K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
A
0
A
3
22 tháng 8 2021
Bài 4:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{5}=\dfrac{y}{6}=\dfrac{x+y}{5+6}=\dfrac{44}{11}=4\)
Do đó: x=20; y=24
2T
4 tháng 9 2019
\(\left|2x+3\right|+2x=-4\)
\(\Leftrightarrow\left|2x+3\right|=-4-2x\)(1)
*Nếu \(x\ge\frac{-3}{2}\)thì \(2x+3\ge0\Rightarrow\left|2x+3\right|=2x+3\)
\(\Rightarrow\left(1\right)\Leftrightarrow2x+3=-4-2x\Leftrightarrow4x=-7\Leftrightarrow x=\frac{-7}{4}\left(L\right)\)
*Nếu \(x< \frac{-3}{2}\)thì \(2x+3< 0\Rightarrow\left|2x+3\right|=-2x-3\)
\(\Rightarrow\left(1\right)\Leftrightarrow-2x-3=-4-2x\Leftrightarrow0=-1\left(L\right)\)
Vậy pt vô nghiệm
4 tháng 9 2019
\(\left|2x+3\right|+2x=-4\)
\(\Leftrightarrow\left|2x+3\right|=-4-2x\)
\(\Leftrightarrow\orbr{\begin{cases}2x+3=-4-2x\\2x+3=-\left(-4-2x\right)\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}2x+2x=-4-3\\2x+3=4+2x\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}4x=-7\\2x-2x=4-3\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-\frac{7}{4}\\0=1\left(loại\right)\end{cases}}\)
Vậy : \(x=-\frac{7}{4}\)
A
2
6 tháng 11 2021
Bài 1:
\(a,=\dfrac{1}{9}\cdot\dfrac{3}{10}+1=\dfrac{1}{30}+1=\dfrac{31}{30}\\ b,=\left(-\dfrac{5}{3}\right)\left(\dfrac{2}{13}+\dfrac{14}{13}-\dfrac{3}{13}\right)=-\dfrac{5}{3}\)
Bài 2:
\(a,\Leftrightarrow\dfrac{2}{5}x=\dfrac{4}{5}-\dfrac{3}{5}=\dfrac{1}{5}\Leftrightarrow x=\dfrac{1}{2}\\ b,\Leftrightarrow\left|2x-\dfrac{2}{3}\right|=\dfrac{4}{3}\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{4}{3}+\dfrac{2}{3}=2\\2x=-\dfrac{4}{3}+\dfrac{2}{3}=-\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\\ c,\Leftrightarrow x^3=-216\Leftrightarrow x=-6\)
T
0
A
2
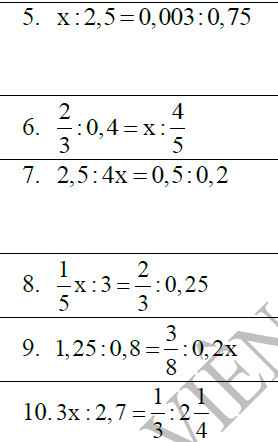
Bài 2:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y+z}{2+3+4}=\dfrac{9}{9}=1\)
Do đó: x=2; y=3; z=4
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{z}{9}=\dfrac{x-3y+4z}{4-3\cdot3+4\cdot9}=\dfrac{62}{31}=2\)
Do đó: x=8; y=6; z=19
c: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+2y-3z}{2+2\cdot3-3\cdot4}=\dfrac{-20}{-4}=5\)
Do đó: x=10; y=15; z=20
Bài 1:
a: Ta có: \(\dfrac{x}{y}=\dfrac{9}{11}\)
nên \(\dfrac{x}{9}=\dfrac{y}{11}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{9}=\dfrac{y}{11}=\dfrac{x+y}{9+11}=\dfrac{60}{20}=3\)
Do đó: x=27; y=33
b: ta có: \(\dfrac{x}{y}=\dfrac{1.2}{2.5}\)
nên \(\dfrac{x}{12}=\dfrac{y}{25}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{12}=\dfrac{y}{25}=\dfrac{y-x}{25-12}=\dfrac{26}{13}=2\)
Do đó: x=24; y=50
c: Ta có: \(7x=4y\)
nên \(\dfrac{x}{4}=\dfrac{y}{7}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{7}=\dfrac{y-x}{7-4}=\dfrac{33}{3}=11\)
Do đó: x=44; y=77
d:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{-7}=\dfrac{y}{4}=\dfrac{2x-3y}{-14-12}=\dfrac{-78}{-26}=3\)
Do đó: x=-21; y=12