
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1,7x-8=4x+7\)
\(\Leftrightarrow7x-8-4x=7\)
\(\Leftrightarrow7x-4x=7+8\)
\(\Leftrightarrow3x=15\)
\(\Rightarrow x=5\)
\(2,3-2x=3\left(x+1\right)-x-2\)
\(\Leftrightarrow3-2x=2x+1\)
\(\Leftrightarrow-2x+3=2x+1\)
\(\Leftrightarrow-2x-2x=1-3\)
\(\Leftrightarrow-4x=-2\)
\(\Rightarrow x=\dfrac{1}{2}\)
\(3,5\left(3x+2\right)=4x+1\)
\(\Leftrightarrow5.3x+5.2=4x+1\)
\(\Leftrightarrow15x+10=4x+1\)
\(\Leftrightarrow15x-4x=1-10\)
\(\Leftrightarrow11x=-9\)
\(\Rightarrow x=\dfrac{-9}{11}\)

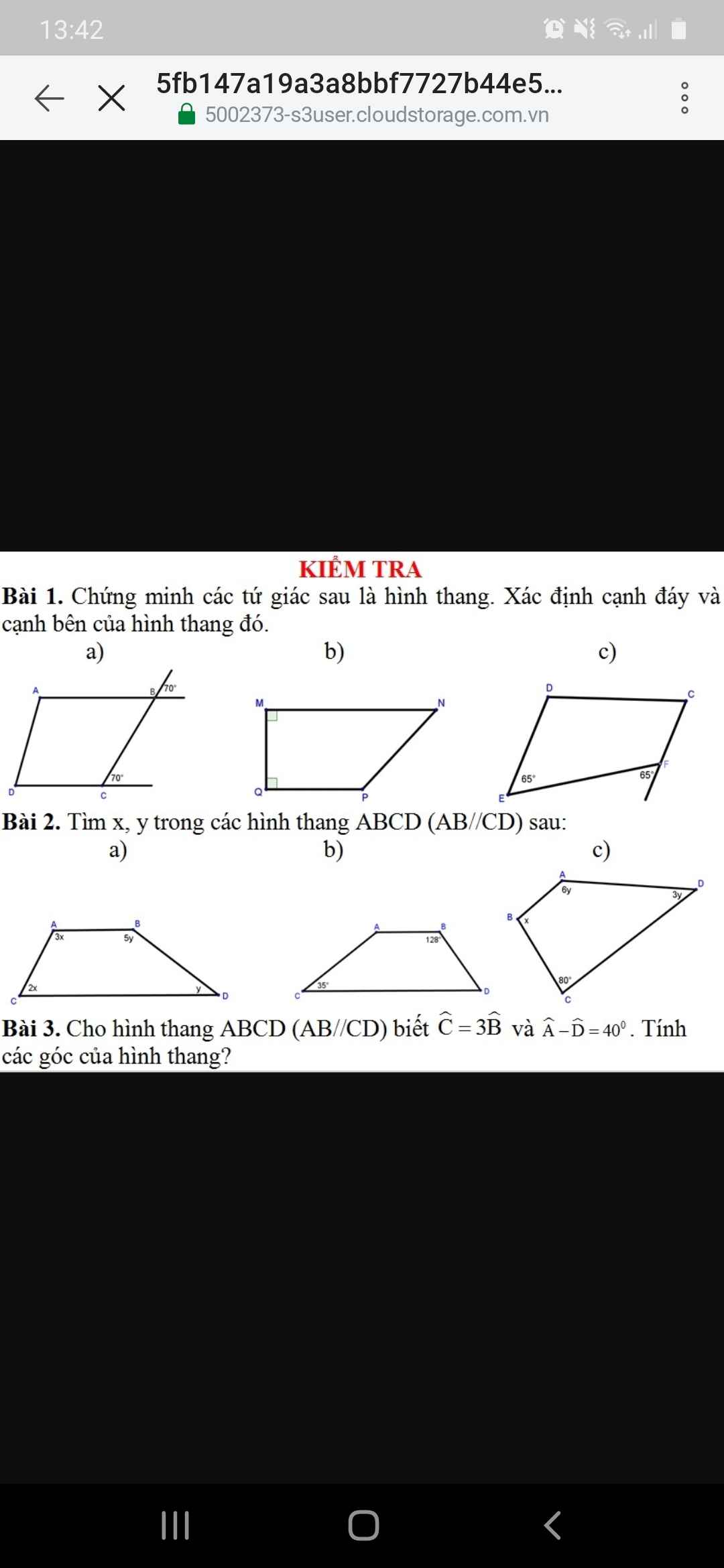
Bài 1
a) góc B=góc C=70 độ(gt)
=>AB//DC(đồng vị)
=> ABCD là hình thang
b)góc M+ góc Q=90 độ +90 độ=180 độ
=>MN//QP( hai góc trong cùng phía bù nhau)
=>MNPQ là hình thang
c)góc E= góc F=65 độ
=>DE//CF( slt)
=> DCFE là hình thang

a, \(40x-20+45x-30=48x-36\Leftrightarrow37x=14\Leftrightarrow x=\dfrac{14}{37}\)
b, đk : x khác -3 ; 3
\(5x+15+4x-12=x-5\Leftrightarrow8x=-38\Leftrightarrow x=-\dfrac{19}{4}\)(tm)
c, \(\left[{}\begin{matrix}2x+3=0\\3x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=\dfrac{1}{3}\end{matrix}\right.\)

1: Ta có: \(A=\dfrac{\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)+1}{x^2+5x+5}\)
\(=\dfrac{\left(x^2+5x+4\right)\left(x^2+5x+6\right)+1}{x^2+5x+5}\)
\(=\dfrac{\left(x^2+5x+5\right)^2}{x^2+5x+5}\)
\(=x^2+5x+5\)

a: Xét tứ giác MIPC có
K là trung điểm của MP
K là trung điểm của IC
Do đó: MIPC là hình bình hành
mà MI=PI
nên MIPC là hình thoi

a: Xét ΔHAC vuông tại H và ΔABC vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔHAC~ΔABC
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>BC=25
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}BH\cdot BC=BA^2\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH\cdot25=15^2=225\\AH\cdot25=15\cdot20=300\end{matrix}\right.\)
=>BH=9; AH=12


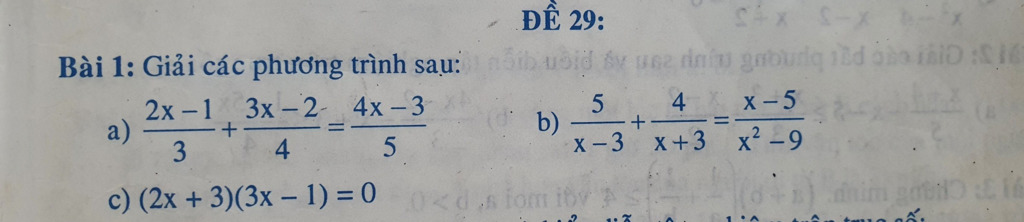


1) \(x^3+y^3+z^3-3xyz=\left(x^3+3x^2y+3xy^2+y^3\right)+z^3-3xyz-3x^2y-3xy^2=\left(x+y\right)^3+z^3-3xy\left(x+y+z\right)=\left(x+y+z\right)\left[\left(x+y\right)^2-\left(x+y\right)z+z^2\right]-3xy\left(x+y+z\right)=\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2\right)-3xy\left(x+y+z\right)=\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2-3xy\right)=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-xz-yz\right)\)
2) Ta có: \(\left(a+b+c\right)^2=a^2+b^2+c^2\)
\(\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ac\right)=a^2+b^2+c^2\)
\(\Leftrightarrow ab+bc+ac=0\)
\(\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}=\dfrac{3}{abc}\)
\(\Leftrightarrow\dfrac{a^3b^3+b^3c^3+a^3c^3}{a^3b^3c^3}=\dfrac{3}{abc}\)
\(\Leftrightarrow\dfrac{a^3b^3+b^3c^3+a^3c^3}{a^2b^2c^2}=3\)
\(\Leftrightarrow a^3b^3+b^3c^3+a^3c^3=3a^2b^3c^2\)
\(\Leftrightarrow\left(ab+bc\right)^3-3ab^2c\left(ab+bc\right)+a^3b^3-3a^2b^2c^2=0\)
\(\Leftrightarrow\left(ab+bc+ac\right)\left[\left(ab+bc\right)^2-\left(ab+bc\right)ac+a^2c^2\right]-3ab^2c\left(ab+bc+ac\right)=0\)
\(\Leftrightarrow0+0=0\left(đúng\right)\)
e cảm ơn ạ