MA
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MA
1
15 tháng 11 2021
a) ĐKXĐ: \(\left\{{}\begin{matrix}2x+3\ne0\\2x+1\ne0\\\left(2x+3\right)\left(2x+1\right)\ne0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ne-\dfrac{3}{2}\\x\ne-\dfrac{1}{2}\\\left(2x+3\right)\left(2x+1\right)\ne0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ne-\dfrac{3}{2}\\x\ne-\dfrac{1}{2}\end{matrix}\right.\)
b) \(\Rightarrow P=\dfrac{2\left(2x+1\right)+3\left(2x+3\right)-6x-5}{\left(2x+3\right)\left(2x+1\right)}\)
\(\Rightarrow P=\dfrac{4x+2+6x+9-6x-5}{\left(2x+3\right)\left(2x+1\right)}\)
\(\Rightarrow P=\dfrac{4x+6}{\left(2x+3\right)\left(2x+1\right)}\)
\(\Rightarrow P=\dfrac{2\left(2x+3\right)}{\left(2x+3\right)\left(2x+1\right)}\)
\(\Rightarrow P=\dfrac{2}{2x+1}\)
c) \(P=-1\Rightarrow\dfrac{2}{2x+1}=-1\\ \Rightarrow2=-2x-1\\ \Rightarrow2x=-3\\ \Rightarrow x=-\dfrac{3}{2}\)
MA
4
14 tháng 11 2021
Bài 6
\(a,ĐK:x\ne\pm5\\ b,P=\dfrac{x-5+2x+10-2x-10}{\left(x-5\right)\left(x+5\right)}=\dfrac{x-5}{\left(x-5\right)\left(x+5\right)}=\dfrac{1}{x+5}\\ c,P=-3\Leftrightarrow\dfrac{1}{x+5}=-3\Leftrightarrow-3\left(x+5\right)=1\Leftrightarrow x=-\dfrac{16}{3}\\ \Leftrightarrow Q=\left(3x-7\right)^2=\left[3\cdot\left(-\dfrac{16}{3}\right)-7\right]^2=529\)
14 tháng 11 2021
Bài 7:
\(a,ĐK:x\ne\pm3\\ b,P=\dfrac{3x-9+x+3+18}{\left(x-3\right)\left(x+3\right)}=\dfrac{4\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{4}{x-3}\\ b,P=4\Leftrightarrow4\left(x-3\right)=4\Leftrightarrow x=4\)
MA
0
15 tháng 11 2021
\(a,=x^2+x+4x+4=\left(x+1\right)\left(x+4\right)\\ b,=x^2+2x-3x-6=\left(x-3\right)\left(x+2\right)\\ c,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ d,=3\left(x^2-2x+5x-10\right)=3\left(x-2\right)\left(x+5\right)\\ e,=-3x^2+6x-x+2=\left(x-2\right)\left(1-3x\right)\\ f,=x^2-x-6x+6=\left(x-1\right)\left(x-6\right)\\ h,=4\left(x^2-3x-6x+18\right)=4\left(x-3\right)\left(x-6\right)\\ i,=3\left(3x^2-3x-8x+5\right)=3\left(x-1\right)\left(3x-8\right)\\ k,=-\left(2x^2+x+4x+2\right)=-\left(2x+1\right)\left(x+2\right)\\ l,=x^2-2xy-5xy+10y^2=\left(x-2y\right)\left(x-5y\right)\\ m,=x^2-xy-2xy+2y^2=\left(x-y\right)\left(x-2y\right)\\ n,=x^2+xy-3xy-3y^2=\left(x+y\right)\left(x-3y\right)\)
MA
3
28 tháng 10 2021
a) \(A=\dfrac{\left(2x^2+2x\right)\left(x-2\right)^2}{\left(x^3-4x\right)\left(x+1\right)}=\dfrac{2x\left(x+1\right)\left(x-2\right)^2}{x\left(x-2\right)\left(x+2\right)\left(x+1\right)}\)
\(=\dfrac{2\left(x-2\right)}{x+2}\)
Thay \(x=\dfrac{1}{2}\) vào A ta được:
\(A=\dfrac{2\cdot\left(\dfrac{1}{2}-2\right)}{\dfrac{1}{2}+2}=\dfrac{-3}{\dfrac{5}{2}}=-\dfrac{6}{5}\)
28 tháng 10 2021
b) \(B=\dfrac{x^3-x^2y+xy^2}{x^3+y^3}=\dfrac{x\left(x^2-xy+y^2\right)}{\left(x+y\right)\left(x^2-xy+y^2\right)}=\dfrac{x}{x+y}\)
Thay \(x=-5,y=10\) vào B ta đc:
\(B=\dfrac{-5}{-5+10}=-1\)
MA
0
MA
1
27 tháng 9 2021
Bài 1:
a) \(=\left(x^2+4x+4\right)-1=\left(x+2\right)^2-1=\left(x+1\right)\left(x+3\right)\)
f) \(=\left(x^2-4x+4\right)-9=\left(x-2\right)^2-3^2=\left(x-5\right)\left(x+1\right)\)
h) \(=x^2\left(x-3\right)-4\left(x-3\right)=\left(x-3\right)\left(x^2-4\right)=\left(x-3\right)\left(x-2\right)\left(x+2\right)\)
k) \(=x^3\left(x-1\right)-\left(x-1\right)\left(x+1\right)=\left(x-1\right)\left(x^3-x-1\right)\)
m) \(=\left(x^4+4x^2+4\right)-9=\left(x^2+2\right)^2-9=\left(x^2-1\right)\left(x^2+5\right)=\left(x-1\right)\left(x+1\right)\left(x^2+5\right)\)
Bài 2:
a) \(=\left(x-y\right)\left(x+y\right)-\left(x+y\right)=\left(x+y\right)\left(x-y-1\right)\)
e) \(=\left(3x-2y\right)\left(9x^2+6xy+4y^2\right)\)
f) giống câu a
g) \(=x^2-2xy=x\left(x-2y\right)\)
i) \(=\left(x^3-y^3\right)\left(x^3+y^3\right)=\left(x-y\right)\left(x^2+xy+y^2\right)\left(x+y\right)\left(x^2-xy+y^2\right)\)
k) \(=\left(x+1\right)^3-27z^3=\left(x+1-3z\right)\left(x^2+2x+1+3xz+3z+9z^2\right)\)
l) \(=\left(2x+1\right)^2-9y^2=\left(2x+1-3y\right)\left(2x+1+3y\right)\)
AM
27 tháng 2 2022
Xét tam giác MNP có MP là đường phân giác của \(\widehat{MNP}\) ta có:
\(\dfrac{MN}{NP}=\dfrac{MF}{FP}\Leftrightarrow\dfrac{MN}{NP}=\dfrac{MF}{MP-MF}\Leftrightarrow\dfrac{6}{10}=\dfrac{MF}{8-MF}\Rightarrow MF=3\left(cm\right)\)\(\Rightarrow FP=8-3=5\left(cm\right)\)
Xét tam giác MNP có ME là đường cao ứng với cạnh huyền, ta có: \(\dfrac{1}{ME^2}=\dfrac{1}{MN^2}+\dfrac{1}{MP^2}\Leftrightarrow\dfrac{1}{ME^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}\Rightarrow ME=4,8\left(cm\right)\)
MA
1
30 tháng 9 2021
a) Đặt \(a=x^2+x\)
Đa thức trở thành: \(a^2-14a+24=\left(a^2-14a+49\right)-25=\left(a-7\right)^2-25=\left(a-7-5\right)\left(a-7+5\right)=\left(a-12\right)\left(a-2\right)\)
Thay a:
\(\left(a-12\right)\left(a-2\right)=\left(x^2+x-12\right)\left(x^2+x-2\right)\)
b) Đặt \(a=x^2+x\)
Đa thức trở thành:
\(\left(x^2+x\right)^2+4x^2+4x-12=\left(x^2+x\right)^2+4\left(x^2+x\right)-12=a^2+4a-12=\left(a^2+4x+4\right)-16=\left(a+2\right)^2-16=\left(a+2-4\right)\left(a+2+4\right)=\left(a-2\right)\left(a+6\right)\)
Thay a:
\(\left(a-2\right)\left(a+6\right)=\left(x^2+x-2\right)\left(x^2+x+6\right)\)
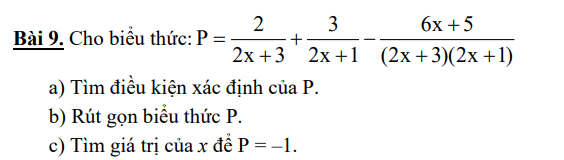
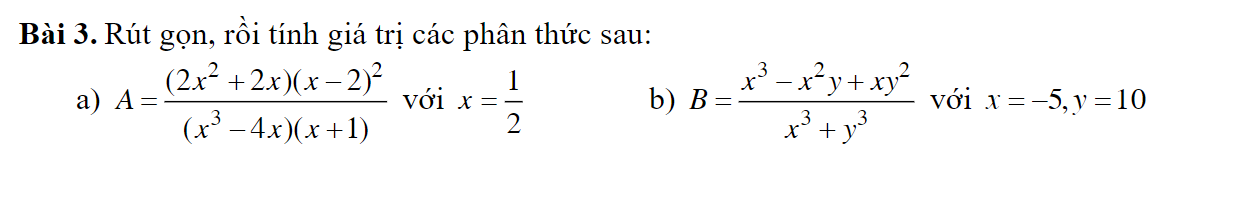
a: Xét tứ giác MIPC có
K là trung điểm của MP
K là trung điểm của IC
Do đó: MIPC là hình bình hành
mà MI=PI
nên MIPC là hình thoi