
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4
a/ \(x=\widehat{ABC};y=\widehat{ADC}\)
Ta có a//b; \(a\perp c\Rightarrow b\perp c\Rightarrow x=\widehat{ABC}=90^o\)
Xét tứ giác ABCD
\(y=\widehat{ADC}=360^o-\widehat{BAD}-\widehat{ABC}-\widehat{BCD}\) (tổng các góc trong của tứ giác = 360 độ)
\(\Rightarrow y=\widehat{ADC}=360^o-90^o-90^o-130^o=50^o\)
b/ Kéo dài n về phí B cắt AC tại D
\(\Rightarrow\widehat{CBD}=180^o-\widehat{nBC}=180^o-105^o=75^o\)
Xét tg BCD có
\(\widehat{BDC}=180^o-\widehat{CBD}-\widehat{BCD}=180^o-75^o-60^o=45^o=\widehat{mAC}\)
=> Am//Bn (Hai đường thẳng bị cắt bởi đường thẳng thứ 3 tạo thành hai góc đồng vị bằng nhau thì chúng // với nhau)
Bài 5
\(\frac{a}{3b}=\frac{b}{3c}=\frac{c}{3a}=\frac{a+b+c}{3\left(a+b+c\right)}=\frac{1}{3}\)
Ta có \(\frac{a}{3b}=\frac{b}{3c}=\frac{a+b}{3\left(b+c\right)}=\frac{1}{3}\Rightarrow\frac{a+b}{b+c}=1\Rightarrow a+b=b+c\)
\(\frac{b}{3c}=\frac{c}{3a}=\frac{b+c}{3\left(c+a\right)}=\frac{1}{3}\Rightarrow\frac{b+c}{c+a}=1\Rightarrow b+c=c+a\)
\(\Rightarrow a+b=b+c=c+a\)
\(\frac{c}{3a}=\frac{a}{3b}=\frac{c+a}{3\left(a+b\right)}=\frac{1}{3}\Rightarrow\frac{c+a}{a+b}=1\)
Từ \(\frac{a+b}{b+c}=\frac{a}{b+c}+\frac{b}{b+c}=\frac{a}{b+c}+\frac{b}{c+a}=1\) (1)
Từ \(\frac{b+c}{c+a}=\frac{b}{c+a}+\frac{c}{c+a}=\frac{b}{c+a}+\frac{c}{a+b}=1\) (2)
Từ \(\frac{c+a}{a+b}=\frac{c}{a+b}+\frac{a}{a+b}=\frac{c}{a+b}+\frac{a}{b+c}=1\) (3)
Công 2 vế của (1) (2) và (3)
\(\Rightarrow\frac{a}{b+c}+\frac{b}{c+a}+\frac{b}{c+a}+\frac{c}{a+b}+\frac{c}{a+b}+\frac{a}{b+c}=3\)
\(\Rightarrow2\left(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\right)=3.\)
\(\Rightarrow\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}=\frac{3}{2}\)
\(\Rightarrow M=2018\left(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\right)=\frac{2018.3}{2}=3027\)



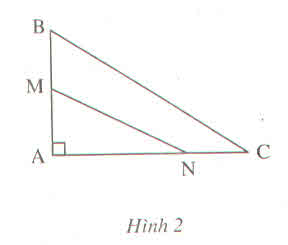
Hình chiếu của AN < hình chiếu của AC
=> đường xiên BN < đường xiên của BC (1)
Hình chiếu của AM < hình chiếu AB => đường xiên MN < đường xiên NB. (2)
Từ (1) và (2) suy ra:
MN< BN< BC.

Giải:
a) \(-1313x^2y.2xy^3\)
\(=\left(-1313.2\right)\left(x^2.x\right)\left(y.y^3\right)\)
\(=-2626x^3y^4\)
Bậc của đơn thức là: \(3+4=7\)
b) \(1414x^3y.\left(-2x^3y^5\right)\)
\(=\left[1414.\left(-2\right)\right]\left(x^3.x^3\right)\left(y.y^5\right)\)
\(=-2828x^6y^6\)
Bậc của đơn thức là: \(6+6=12\).
Chúc bạn học tốt!!!
a) -x2y. 2xy3 = -2x3y4. Đơn thức có bậc là 7
b) x3y. (-2x3y5) = -2x6y6. Đơn thức có bậc là 12

\(3^{x+1}+3^{x+3}=810\)
\(\Leftrightarrow3^{x+1}+3^{x+1}.3^2=810\)
\(\Leftrightarrow3^{x+1}.10=810\)
\(\Leftrightarrow3^{x+1}=81=3^4\)
\(\Leftrightarrow x+1=4\)
\(\Leftrightarrow x=3\)


Ta có : a song song với b
=> Góc A = Góc B = 90độ
Hay x = 90 độ
=> Góc D + Góc C = 180độ ( 2 góc trong cùng phía )
=> y + 130 độ = 180 độ
=> y = 50 độ
Vẽ Cx song song với Am(1), ta được :
=> Góc mAC + Góc ACx = 180 độ
=> Góc mAC + Góc BCA + Góc BCx = 180 độ
Hay Góc BCx = 180 độ - 45 độ - 60 độ = 75 độ
Vì Góc nBC + Góc BCx = 180 độ ( 75 độ + 105 độ = 180 độ )
Mà Góc nBC và Góc BCx là 2 góc trong cùng phía
Nên ta được Bn song song với Cx (2)
Từ (1) và (2) => Bn song song với Am

BT1.
Ta có: \(2009^{20}=2009^{10}\times2009^2\)và \(20092009^{10}=2009^{10}\times10001^{10}\)
Rõ ràng \(2009^2< 10001^{10}\\ \Rightarrow2009^{10}\times2009^2< 2009^{10}\times10001^{10}\\ \Rightarrow2009^{20}< 20092009^{10}\left(đpcm\right)\)
BT9. Bn xem lại đề bài đi. \(x^2+x+1\) luôn lớn hơn 0 mà bn.
BT3.
Giả sử \(M\in N\)
Nên:
\(\left\{{}\begin{matrix}\dfrac{x}{x+y+z}\in N\\\dfrac{y}{y+x+t}\in N\\\dfrac{z}{z+t+y}\in N\\\dfrac{t}{t+z+x}\in N\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x⋮x+y+z\\y⋮y+x+t\\z⋮z+t+y\\t⋮t+z+x\end{matrix}\right.\)
Vì \(x,y,z,t\in N\)*\(\Rightarrow x,y,z,t>0\)\(\Rightarrow\left\{{}\begin{matrix}x>x+y+z\\y>x+y+t\\z>y+z+t\\t>x+z+t\end{matrix}\right.\)(vô lí)
Vậy rõ ràng điều giả sử là vô lí. Nên \(M\notin N\left(đpcm\right)\)
Mình chỉ giúp đc đến đây thôi, mong bn thông cảm
Ngoài ra, chúc bn học tốt nhé![]()
![]()
![]()
![]()
![]()
Bài toán 2.
Ta có: \(B=\dfrac{2008}{1}+\dfrac{2007}{2}+\dfrac{2006}{3}+....+\dfrac{2}{2007}+\dfrac{1}{2008}\)
\(=\dfrac{2009-1}{1}+\dfrac{2009-2}{2}+\dfrac{2009-3}{3}+...+\dfrac{2009-2008}{2008}\)
\(=2009-1+\dfrac{2009}{2}-1+\dfrac{2009}{3}-1+....+\dfrac{2009}{2008}-1\)
\(=2009+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{....1}{2008}\right)-1.2008\)
\(=\left(2009-2008\right)+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+....+\dfrac{1}{2008}\right)\)
\(=1+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+....+\dfrac{1}{2008}\right)\)
\(=2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2008}+\dfrac{1}{2009}\right)\)
=\(2009.A\)
Do đó, tỉ số \(\dfrac{A}{B}=\dfrac{A}{2009.A}=\dfrac{1}{2009}\)




 mn giúp mk vs, mk cần gấp!!!cảm ơn trước ạ
mn giúp mk vs, mk cần gấp!!!cảm ơn trước ạ mn giải giúp mik bài 1 và bài 2a với, mik đag cần gấp, mik cảm ơn mn nhiều
mn giải giúp mik bài 1 và bài 2a với, mik đag cần gấp, mik cảm ơn mn nhiều





Ta thấy các PS đều có dạng: \(\dfrac{1}{1+\left(n+2\right)},\dfrac{2}{2+\left(n+2\right)},...,\dfrac{p-2}{p-2+\left(n+2\right)},\dfrac{p-1}{p-1+\left(n+2\right)}\)Tức là có dạng \(\dfrac{p}{p+\left(n+2\right)}\)
⇒ p và n+2 là nguyên tố cùng nhau
Thế thì p là số nguyên tố nào z
:v ủa vậy nói k mấy đi :v