
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.Xét tam giác vuông AED và tam giác vuông AFD, có:
A: góc chung
AD: cạnh chung
Vậy tam giác vuông AED = tam giác vuông AFD ( cạnh huyền . góc nhọn)
=> DE = DF ( 2 cạnh tương ứng )
b.Xét tam giác vuông BDE và tam giác vuông CDF, có:
góc B = góc C ( gt )
DE = DF ( cmt )
Vậy tam giác vuông BDE = tam giác vuông CDF ( góc nhọn. cạnh góc vuông )
c. ta có: AD là đường phân giác trong tam giác cân ABC cũng là đường trung trực
=> AD là đường trung trực của BC
Chúc bạn học tốt!!!

\(2^{x+2}-2^x=96\)
\(\Rightarrow2^x.2^2-2^x=96\)
\(\Rightarrow2^x\left(2^2-1\right)=96\)
\(\Rightarrow2^x.3=96\)
\(\Rightarrow2^x=32\Rightarrow2^x=2^5\Rightarrow x=5\)

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó; ΔABM=ΔACM
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: AE=AF và ME=MF
hay ΔMEF cân tại M
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC

Bài 7:
\(A\le-5.9\forall x\)
Dấu '=' xảy ra khi x=1,34

a: góc yOz=180-60=120 độ
góc zOm=góc yOm=120/2=60 độ
b: góc xOn=góc zOm=60 độ
=>góc xOn=góc xOy
=>Ox là phân giác của góc yOn


#\(N\)
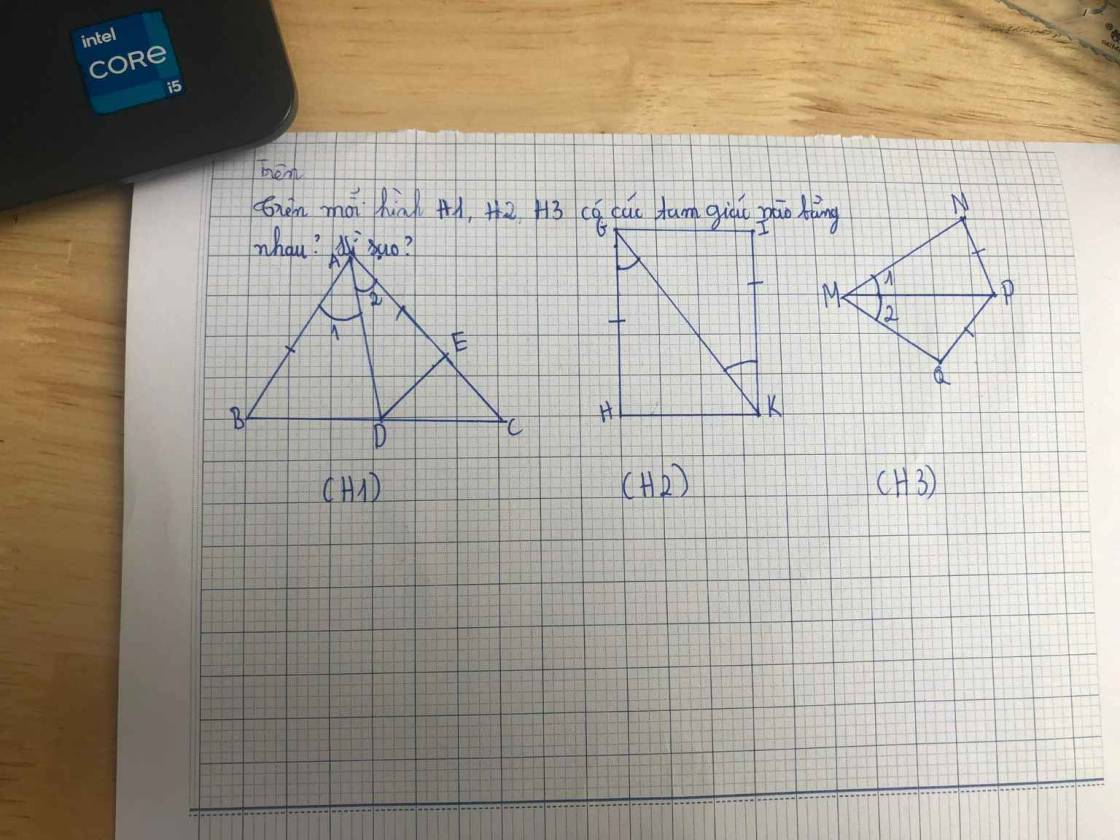
`H1,`
Xét Tam giác `ADB` và Tam giác `ADE`có:
`AB = AE`
\(\widehat{BAD}=\widehat{EAD}\)
`AD` chung
`=>` Tam giác `ADB = ` Tam giác `ADE (c-g-c)`
`H2,` Xét Tam giác `HGK` và Tam giác `IKG` có:
`HG = IK`
\(\widehat{HGK}=\widehat{IKG}\)
`GK` chung
`=>` Tam giác `HGK =` Tam giác `IKG (c-g-c)`
`H3,` Không có tam giác nào bằng nhau (vì 2 tam giác trên không có đủ yếu tố)
*ps: lần sau vẽ hình cân đối hơn cậu nha .-.


Bài 1:
Ta có: \(4x^5y^2-3x^3y+7x^3y+ax^5y^2\)
\(=\left(a+4\right)\cdot x^5y^2+4x^3y\)
Để đa thức có bậc bằng 4 thì a+4=0
hay a=-4
Vậy: a=-4


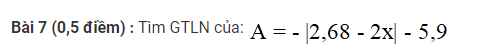

 giải hộ bài này với ạ
giải hộ bài này với ạ



a) Do AB < AC (gt)
⇒ ∠C < ∠B (quan hệ giữa góc và cạnh đối diện trong tam giác)
b) Xét hai tam giác vuông: ∆ABM và ∆EBM có:
AB = BE (gt)
BM là cạnh chung
⇒ ∆ABM = ∆EBM (cạnh huyền - cạnh góc vuông)
c) Do ME ⊥ BC (gt)
⇒ NE ⊥ BC
⇒ NE là đường cao của ∆BCN
Do ∆ABC vuông tại A (gt)
⇒ CA ⊥ AB
⇒ CA ⊥ NB
⇒ CA là đường cao thứ hai của ∆BCN
Mà M là giao điểm của NE và CA
⇒ BM là đường cao thứ ba của ∆BCN
⇒ BM ⊥ NC