Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

OLM chào em và cảm ơn em đã yêu thương và tin tưởng và lựa chọn hệ thống giáo dục olm.vn.
Về vấn đề em hỏi cô xin chia sẻ tới em một vài thông tin như sau:
+ Em cần phải xem kỹ xem yêu cầu đổi quà của em đã thành công hay chưa?
+ Nếu chưa thành công thì tức là em sẽ không nhận được quà vì hệ thống chưa xác nhận yêu cầu đổi quà của em.
+ Nếu yêu cầu đổi quà em đã đực xác thực hệ thống sẽ thông báo tới em là yêu cầu đổi quà thành công.
+ Em cần kiểm tra địa chỉ của em xem đã đúng chưa, tất cả mọi thứ đều chuẩn mực em sẽ nhận được quà từ olm em nhé.
+ Nếu các thông tin em cung cấp không chính xác thì quà sẽ bị gửi lại công ty và em không nhận được quà.
Trên đây là các thông tin mà cô gửi đến em về việc đổi quà, bản thân cô cũng nhận được rất nhiều quà từ olm nên em cứ yên tâm nhá.

Giới hạn đến 2- thì là x nhỏ hơn 2, giới hạn đến 2+ thì là lớn hơn 2
Mà thật ra là bạn chỉ nên quan đến khi x tiến đến 2- hay 2+ khi có dấu căn hoặc là giá trị tuyệt đối thôi, còn trong những dạng này thì thay như bình thường. Mẫu bằng 0 thì xem trên tử, tử bằng 0 thì biến đổi hoặc tử khác 0 thì sẽ ra kết quả luôn
\(\lim\limits_{x\rightarrow2^-}\dfrac{3x^2+x-1}{2x^2-5x+2}\)
\(=+\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow2^-}3x^2+x-1=3\cdot2^2+2-1=3\cdot4+1=13>0\\\lim\limits_{x\rightarrow2^-}2x^2-5x+2=2\cdot2^2-5\cdot2+2=0\\\end{matrix}\right.\)
Giới hạn 1 phía thì gần như bạn kia nói (mặc dù cuối cùng lại kết luận sai). Với \(x\rightarrow2^-\) thì đồng nghĩa \(x< 2\), nên khi đó nhìn lên khu vực xét dấu của \(2x^2-5x+2\) ta sẽ biết nó âm hay dương.
Nếu giới hạn \(x\rightarrow2\) mà tử, mẫu có cùng nhân tử \(x-2\) (nghĩa là rút gọn được) thì làm bình thường. Còn nếu chỉ có mẫu tiến tới 0, tử tiến tới 1 số khác 0 thì có thể kết luận ngay là giới hạn này ko tồn tại (ngoại trừ trường hợp dấu của mẫu số ko đổi khi x đi qua 2, ví dụ như \(\left(2x^2-5x+2\right)^2\) thì nó luôn dương, hoặc \(\left|2x^2-5x+2\right|\) cũng vậy)
Ví dụ cụ thể: \(\lim\limits_{x\rightarrow2^-}\dfrac{3x^2+x-1}{2x^2-5x+2}=-\infty\)
\(\lim\limits_{x\rightarrow2}\dfrac{3x^2+x-1}{2x^2-5x+2}\) không tồn tại.
\(\lim\limits_{x\rightarrow2}\dfrac{3x^2+x-1}{\left|2x^2-5x+2\right|}=+\infty\)
\(\lim\limits_{x\rightarrow2}\dfrac{3x^2+x-1}{-\left(2x^2-5x+2\right)^2}=-\infty\)
Theo định nghĩa về giới hạn tại 1 điểm: giới hạn tại 1 điểm chỉ tồn tại khi giới hạn trái và giới hạn phải tại đó bằng nhau.
Nghĩa là muốn \(\lim\limits_{x\rightarrow a}f\left(x\right)\) thì \(\lim\limits_{x\rightarrow a^+}f\left(x\right)=\lim\limits_{x\rightarrow a^-}f\left(x\right)\)
Trong ví dụ của em \(\lim\limits_{x\rightarrow2^-}f\left(x\right)=-\infty\) còn \(\lim\limits_{x\rightarrow2^+}f\left(x\right)=+\infty\)
Rõ ràng là \(-\infty\ne+\infty\) nên \(\lim\limits_{x\rightarrow2}\dfrac{3x^2+x-1}{2x^2-5x+2}\) ko tồn tại

a) ĐK: \(\cos x\ne0\)( vì tan x = sinx/cosx nên cos x khác 0)
<=> \(x\ne\frac{\pi}{2}+k\pi\); k thuộc Z
TXĐ: \(ℝ\backslash\left\{\frac{\pi}{2}+k\pi\right\}\); k thuộc Z
b) ĐK: \(1+\cos2x\ne0\Leftrightarrow\cos2x\ne-1\Leftrightarrow2x\ne\pi+k2\pi\Leftrightarrow x\ne\frac{\pi}{2}+k\pi\); k thuộc Z
=> TXĐ: \(ℝ\backslash\left\{\frac{\pi}{2}+k\pi\right\}\); k thuộc Z
c) ĐK: \(\hept{\begin{cases}\cot x-\sqrt{3}\ne0\\\sin x\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ne\frac{\pi}{6}+k\pi\text{}\text{}\\x\ne l\pi\end{cases}}\); k,l thuộc Z
=>TXĐ: ....
d) ĐK: \(1-2\sin^2x\ne0\Leftrightarrow\cos2x\ne0\Leftrightarrow2x\ne\frac{\pi}{2}+k\pi\Leftrightarrow x\ne\frac{\pi}{4}+\frac{k\pi}{2}\)
=> TXĐ:...


👍🏻 Cách 1.
Như trên hình là số thứ tự các ghế
❤️ Trường hợp 1
Ghế có số lẻ là ghế các bạn nữ thì
G1 có 4 lựa chọn
G3 có 3 lựa chọn
G5 có 2 lựa chọn
G1 có 1 lựa chọn
Các ghế chẵn là nam
G2 có 4 lựa chọn
G4 có 3 lựa chọn
G6 có 2 lựa chọn
G8 có 1 lựa chọn
==> Với trường hợp 1 sẽ có
(4x3x2x1)x(4x3x2x1)=576 cách xếp
❤️ Trường hợp 2
Các ghế lẻ là nam và các ghế chẵn là nữ thì tương tự ta cũng có 576 cách xếp
=> Với cách 1 ta có
2x576=1152 cách xếp
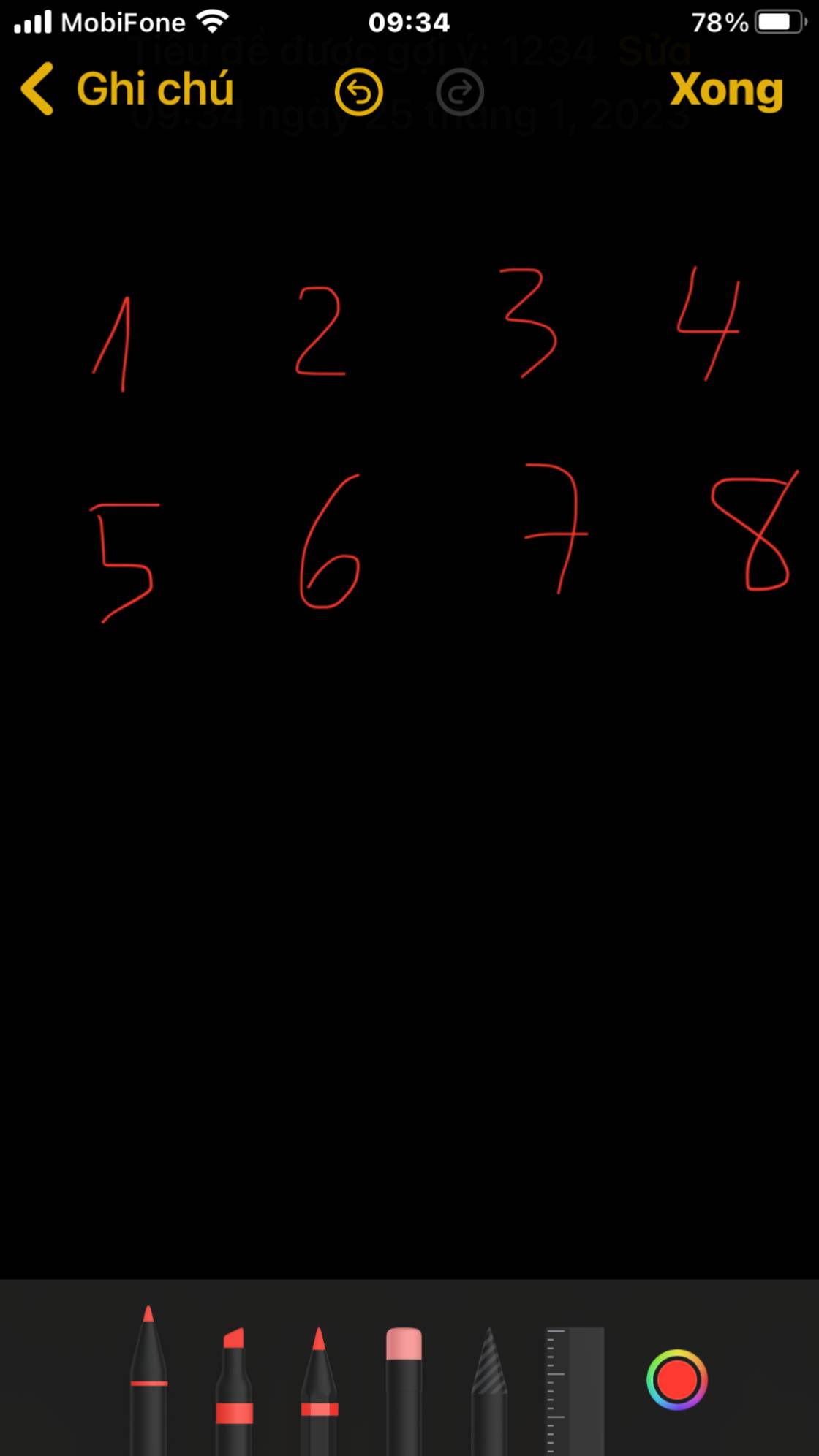
Cách 2 xếp 2 bàn ngược lại với cách 1 thì ta cũng sẽ có
1152 cách xếp
=> Với 2 cách xếp + 4 trường hợp ta có
2x1152=2304 cách xếp



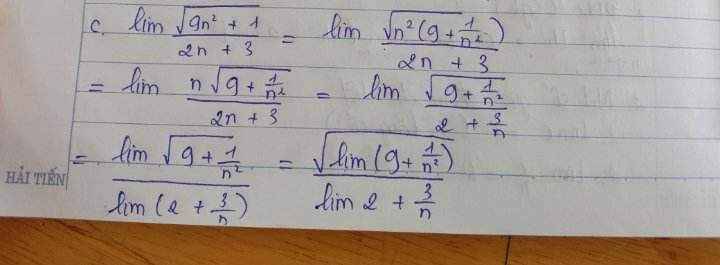

Đây là 1 lời giải sai em
Đơn giản vì phương trình gốc không thể giải được
Em cảm ơn ạ