
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\dfrac{3}{4}+\dfrac{9}{5}\div\dfrac{3}{2}-1=\dfrac{3}{4}+\dfrac{18}{15}-1=\dfrac{39}{20}-1=\dfrac{19}{20}\)
b) \(\dfrac{6}{7}\cdot\dfrac{8}{13}+\dfrac{6}{13}\cdot\dfrac{9}{7}-\dfrac{4}{13}\cdot\dfrac{6}{7}=\dfrac{48}{91}+\dfrac{54}{91}-\dfrac{24}{91}=\dfrac{48+51-24}{91}=\dfrac{78}{91}=\dfrac{6}{7}\)
c) \(\dfrac{-3}{7}+\left(\dfrac{3}{-7}-\dfrac{3}{-5}\right)\)\(=\dfrac{-3}{7}+\left(\dfrac{-3}{7}-\dfrac{-3}{5}\right)=\dfrac{-3}{7}+\dfrac{6}{35}=-\dfrac{9}{35}\)

a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật

a: Xét tứ giác MDHE có
\(\widehat{MDH}=\widehat{MEH}=\widehat{EMD}=90^0\)
Do đó: MDHE là hình chữ nhật


a: 3x+4<-2
=>3x<-6
=>x<-2
b: =>3(x+2)-12>2(x-1)
=>3x+6-12>2x-2
=>3x-6>2x-2
=>x>4

\(A=\left(\frac{x}{x+2}+\frac{x^3}{\left(x+2\right)\left(x^2-2x+4\right)}.\frac{x^2-2x+4}{4-x^2}\right):\frac{4}{x+2}\)
\(A=\left(\frac{x}{x+2}+\frac{x^3}{x+2\left(4-x^2\right)}\right):\frac{4}{x+2}\)
\(A=\left(\frac{4x-x^3+x^3}{x+2\left(4-x\right)}\right):\frac{4}{x+2}\)
\(A=\frac{4x}{x+2\left(4-x\right)}.\frac{x+2}{4}\)
\(A=\frac{x}{4-x}\)
\(b,\frac{x}{4-x}>0\)
xét 2 trường hợp x>0 đồng thời 4-x>0 (điều kiện x\(\ne\)4) và x<0 ,4-x<0
\(TH1:0< x< \text{4}\)
\(TH2:\)ko có giá trị x
\(c,Ax=\frac{x}{4-x}x\)=\(\frac{x^2}{4-x}\)
\(\frac{x^2-16+16}{4-x}\)
\(\frac{\left(x-4\right)\left(x+4\right)+16}{4-x}\)
\(-\left(x+4\right)+\frac{16}{4-x}\)
để AX nguyên thì \(16⋮4-x\)
lập bảng ra tìm đc x = 0,2,-4,-12,5,6,8,12,20

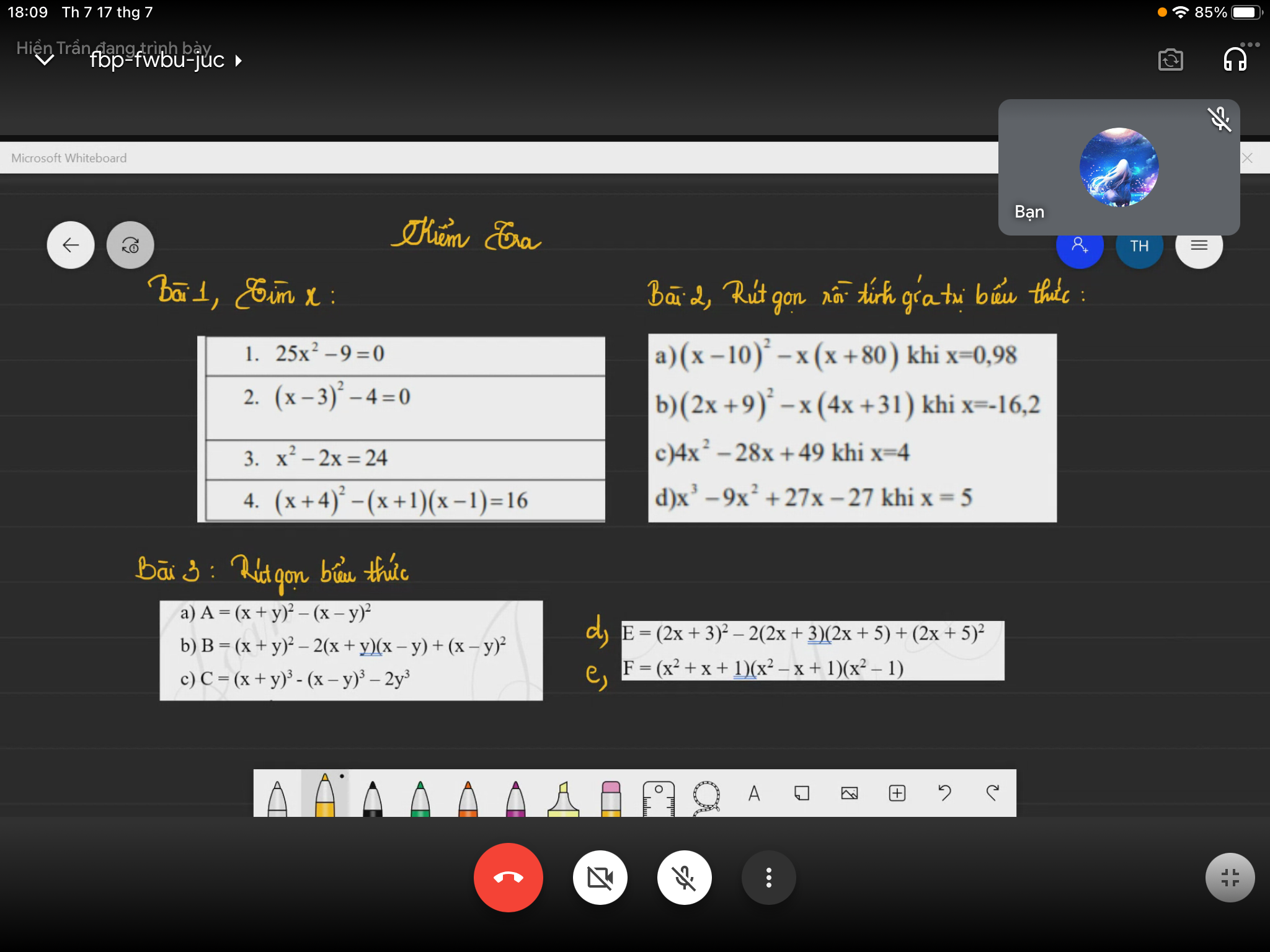
Bài 3:
a) Ta có: \(A=\left(x+y\right)^2-\left(x-y\right)^2\)
\(=x^2+2xy+y^2-\left(x^2-2xy+y^2\right)\)
\(=x^2+2xy+y^2-x^2+2xy-y^2\)
=4xy
b) Ta có: \(B=\left(x+y\right)^2-2\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\)
\(=\left(x+y-x+y\right)^2\)
\(=\left(2y\right)^2=4y^2\)
c) Ta có: \(C=\left(x+y\right)^3-\left(x-y\right)^3-2y^3\)
\(=x^3+3x^2y+3xy^2+y^3-\left(x^3-3x^2y+3xy^2-y^3\right)-2y^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3-2y^3\)
\(=6x^2y\)

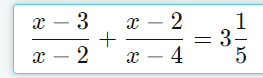 mình cần gấp giúp mình với
mình cần gấp giúp mình với

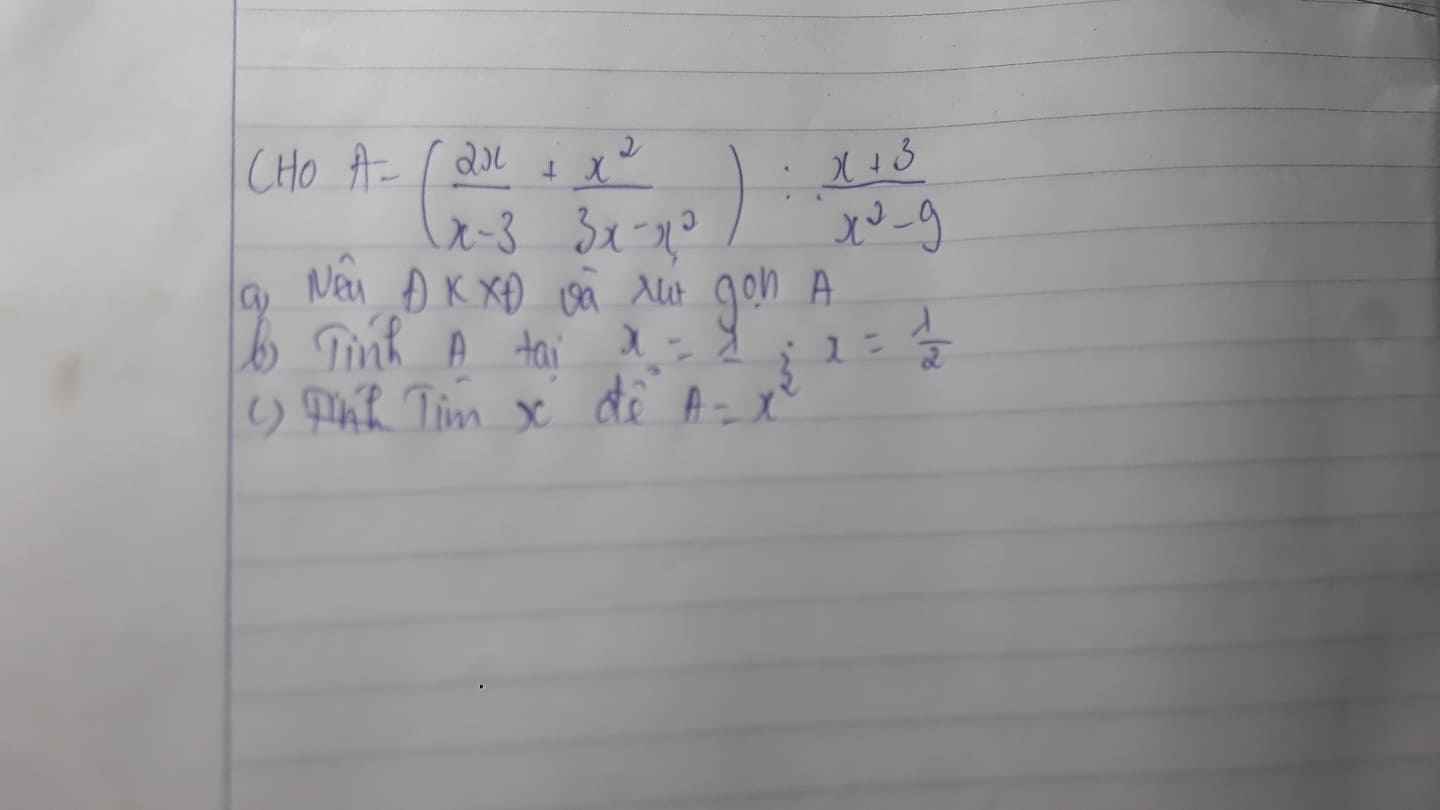




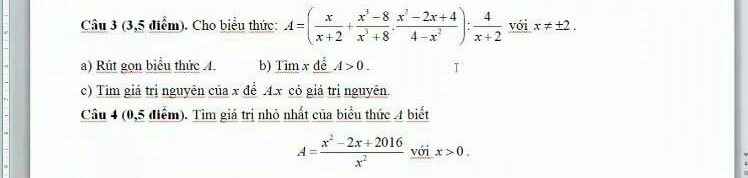

Điều kiện : \(x\in\left\{2,4\right\}\)
Biến đổi PT về dạng :
\(5\left(x-3\right)\left(x-4\right)+5\left(x-2\right)^2=16\left(x-2\right)\left(x-4\right)\)
\(\Leftrightarrow5\left(x^2-7x+12\right)+5\left(x^2-4x+4\right)=16\left(x^2-6x+8\right)\)
\(\Leftrightarrow6x^2-41x+48=0\Leftrightarrow6x^2-9x-32x+48=0\)
\(\Leftrightarrow6x\left(x-\dfrac{3}{2}\right)-32\left(x-\dfrac{3}{2}\right)=0\Leftrightarrow\left(x-\dfrac{3}{2}\right)\left(6x-32\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{3}{2}=0\\6x-32=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{16}{3}\end{matrix}\right.\)
Vậy PT có nghiệm ...
Đáp số là x=1,5 nhé