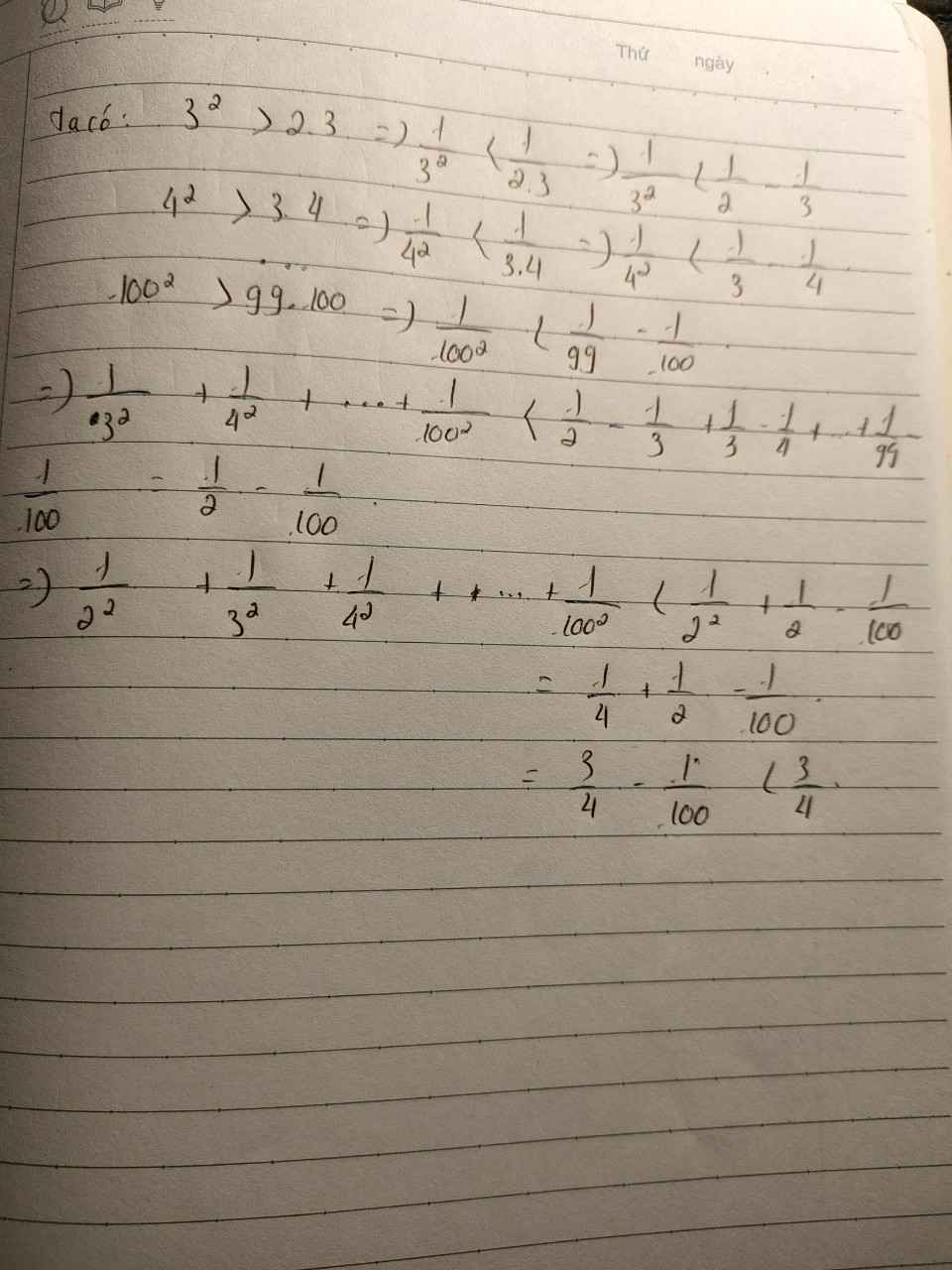Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A=1/3^2+1/4^2+1/5^2+1/6^2+...+1/100^2<1/2-1/3+1/3-1/4+...+1/99-1/100
=>A<1/2-1/100<1/2

Không phải chỉ là khi rút gọn mà trong khi thực hiện phép tính em cũng cần đưa về mẫu số dương em nhé.

a) Ta có: \(\dfrac{39}{-65}=\dfrac{-39}{65}=\dfrac{-39:13}{65:13}=\dfrac{-3}{5}\)
\(\dfrac{-3}{5}=\dfrac{-3}{5}\)
Do đó: \(\dfrac{-3}{5}=\dfrac{39}{-65}\)
b) Ta có: \(\dfrac{-9}{27}=\dfrac{-9:9}{27:9}=\dfrac{-1}{3}\)
\(\dfrac{-41}{123}=\dfrac{-41:41}{123:41}=\dfrac{-1}{3}\)
Do đó: \(\dfrac{-9}{27}=\dfrac{-41}{123}\)
c) Ta có: \(\dfrac{-3}{4}=\dfrac{-3\cdot5}{4\cdot5}=\dfrac{-15}{20}\)
\(\dfrac{4}{-5}=\dfrac{-4}{5}=\dfrac{-4\cdot4}{5\cdot4}=\dfrac{-16}{20}\)
mà \(\dfrac{-15}{20}>\dfrac{-16}{20}\)
nên \(\dfrac{-3}{4}>\dfrac{4}{-5}\)
d) Ta có: \(\dfrac{2}{-3}=\dfrac{-2}{3}=\dfrac{-2\cdot7}{3\cdot7}=\dfrac{-14}{21}\)
\(\dfrac{-5}{7}=\dfrac{-5\cdot3}{7\cdot3}=\dfrac{-15}{21}\)
mà \(\dfrac{-14}{21}>\dfrac{-15}{21}\)
nên \(\dfrac{2}{-3}>\dfrac{-5}{7}\)

Đặt \(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{99^2}+\dfrac{1}{100^2}\)
\(< \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{98.99}+\dfrac{1}{99.100}\)
\(B=\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{98.99}+\dfrac{1}{99.100}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{98}-\dfrac{1}{99}+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=1-\dfrac{1}{100}=\dfrac{99}{100}\) \(\Rightarrow A< \dfrac{99}{100}\)
\(1-\dfrac{1}{2^2}-\dfrac{1}{3^2}-...-\dfrac{1}{100^2}=1-\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}\right)=1-A>\dfrac{1}{100}\)

1/4^2 + 1/5^2 +... + 1/100^2 < 1/3.4 + 1/4.5 +...+ 1/99.100
A=1/3 - 1/4 + 1/4 - 1/5 +...+ 1/99 - 1/100
=1/3 - 1/100 < 1/3

A = \(\dfrac{1}{2^2}\) + \(\dfrac{1}{4^2}\) + \(\dfrac{1}{6^2}\) + .....+ \(\dfrac{1}{1002^2}\)
A = \(\dfrac{1}{2^2.1^2}\) + \(\dfrac{1}{2^2.2^2}\) + \(\dfrac{1}{2^2.3^2}\)+......+\(\dfrac{1}{2^2.501^2}\)
A = \(\dfrac{1}{2^2}\) \(\times\)( \(1\) + \(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\)+.......+ \(\dfrac{1}{501^2}\))
ta có : \(\dfrac{1}{2^2}\) < \(\dfrac{1}{1.2}\)
\(\dfrac{1}{3^2}\) < \(\dfrac{1}{2.3}\)
................
\(\dfrac{1}{501^2}\) < \(\dfrac{1}{500.501}\)
Cộng vế với vế ta được
\(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\) +.....+ \(\dfrac{1}{501^2}\) < \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+.......+\dfrac{1}{500.501}\)
\(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\) +.....+ \(\dfrac{1}{501^2}\) < \(\dfrac{1}{1}\) - \(\dfrac{1}{2}\) + \(\dfrac{1}{2}-\dfrac{1}{3}\)+.....+ \(\dfrac{1}{500}-\dfrac{1}{501}\)
\(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\)+......+ \(\dfrac{1}{501^2}\) < 1 - \(\dfrac{1}{501}\) < 1
=>A = \(\dfrac{1}{4}\) \(\times\) ( 1 + \(\dfrac{1}{2^2}\)+ \(\dfrac{1}{3^2}\)+.....+\(\dfrac{1}{501^2}\)) < \(\dfrac{1}{4}\) \(\times\)(1 + 1)
A < \(\dfrac{1}{4}\) \(\times\) 2
A < \(\dfrac{1}{2}\)