Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

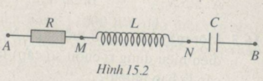
Ta vẽ giản đồ vectơ : U → = U A M → + U M N → + U N B →
Trong đó U A M → ↑ ↑ I → ; U N B → ⊥ I →
Hai tam giác ABM và NBM bằng nhau (có các cạnh lần lượt bằng nhau) dẫn tới kết quả hai tam giác vuông HAB và HNM đồng dạng, suy ra
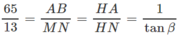
⇒ tan β = 16/65 = 1/5
Trên Hình 15.1.G
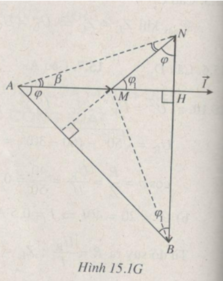
2 β = φ 1
⇒ sin φ 1 = sin2 β
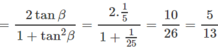
Mặt khác theo Hình 15.1G, ta có :
φ + φ1 = π/2 ⇒ cosφ = sinφ1 = 5/13

Chọn đáp án D
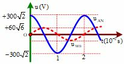
+ Từ đồ thị ta có: 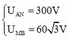 và vuông pha
và vuông pha
![]()
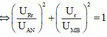
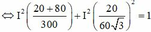
![]()
+ Kết hợp với giản đồ véc tơ, với
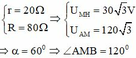
U = 275V

Chọn đáp án A
Mạch điện:
![]()
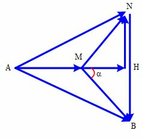
Giản đồ vecto của mạch:
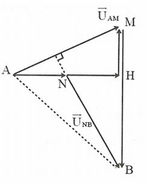
Theo đề bài ta có: U N B = U A M ⇒ N B = A M ∠ A M H = ∠ B H N
⇒ Δ A H M = Δ B H N (cạnh huyền và góc nhọn bằng nhau)
Suy ra:
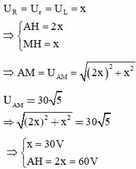
Mà:
Δ A H M = Δ B H N ⇒ A H = H B = 2 x = 60
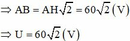

Giải thích: Đáp án A
Mạch điện:
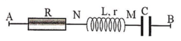
Giản đồ vectơ của mạch:
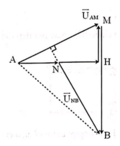
Theo đề bài ta có:


Đáp án: B
Sử dụng các công thức của bài toán điện dung của tụ điện thay đổi.
Điều chỉnh C để điện áp hiệu dụng hai đầu tụ đạt giá trị cực đại thì uRL vuông pha với u.
Ta có giản đồ véc tơ như hình bên
Khi đó u R L 2 U 0 R L 2 + u 2 U 0 2 = 1 ⇔ 50 2 . 6 U 0 R L 2 + 150 2 . 6 U 0 2 = 1 (1)
Mặt khác, từ hệ thức lượng trong tam giác vuông ta có:
1
U
0
R
L
2
+
1
U
0
2
=
1
U
0
R
2
=
1
150
2
.
2
(2)
Giải (1) và (2) ta thu được U 0 2 = 180000 ⇒ U 0 = 300 2 ⇒ U = 300 (V)

Đáp án B
Phương pháp giải: Sử dụng các công thức của bài toán điện dung của tụ điện thay đổi.
Điều chỉnh C để điện áp hiệu dụng hai đầu tụ đạt giá trị cực đại thì uRL vuông pha với u.
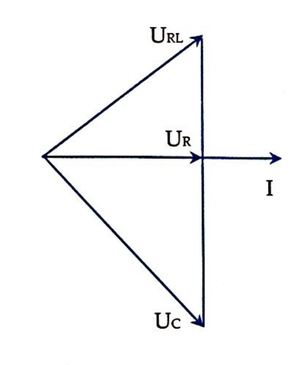


Chọn D.
U = U R 2 + U L − U C 2 = 13 2 + 13 − 65 2 = 13 17 ≠ U
để cho cuộn dây có trở kháng r
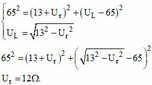
k = cos φ = U R + U r U = 13 + 12 65 = 5 13 .

Khi tụ điện bị nối tắt (H.III.6.G)
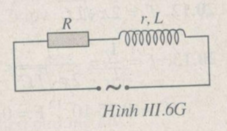
![]()
⇒ r 2 + Z L 2 = 60 2
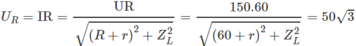
Kết hợp với (a) : r = 30 Ω và Z L = 30 3 Ω
Khi tụ điện không bị nỗi tắt :
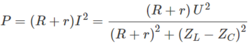
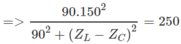
⇒ Z L - Z C = 0 ⇒ Z L = Z C = 30 3 Ω

Theo bài ra ta có
U 2 = U R 2 + U C - U L 2
![]()
cos φ = R/Z = U R /U = 40/50 = 0,8
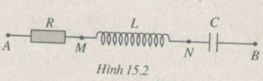
Ta thấy cuộn dây không thuần cảm vì : U 2 ≠ U A M 2 + U N B - U M N 2