Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: D
Ta có: ZL = 60Ω; ZC = 20Ω
Tổng trở của mạch:
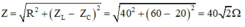
Biểu thức của i:
Ta có: u = 240√2cos100πt (V) → i = I0cos(100πt + φi)
Với 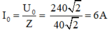
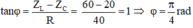
→ φ = φu – φi → φi = φu – φ = 0 – π/4 = – π/4 rad
Vậy i = 6cos(100πt – π/4) (A)

Ta có: \(Z_L=L\omega=100\left(\Omega\right)\)
\(Z_C=\dfrac{1}{C\omega}=200\left(\Omega\right)\)
\(\Rightarrow Z=\sqrt{\left(R+r\right)^2+\left(Z_L-Z_C\right)^2}=100\sqrt{2}\left(\Omega\right)\)
Có: \(U_0=I_0.Z=200\sqrt{2}\left(V\right)\)
\(\tan\varphi=\dfrac{Z_L-Z_C}{R+r}=-1\) \(\Rightarrow\varphi=-\dfrac{\pi}{4}=\varphi_u-\varphi_i\) \(\Rightarrow\varphi_u=-\dfrac{5\pi}{12}\)
Vậy: \(u=200\sqrt{2}\cos\left(100\pi t-\dfrac{5\pi}{12}\right)\)
→ Đáp án: C
Bạn tham khảo nhé!

- Biểu diễn điện áp tức thời ở hai đầu tụ điện dưới dạng số phức:
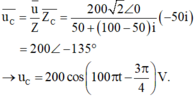

Cảm kháng \(Z_L=Lw=\dfrac{1}{\pi}\cdot100\pi=100\left(\Omega\right)\)
Dung kháng \(Z_C=\dfrac{1}{Cw}=\dfrac{1}{\dfrac{10^{-4}}{2\pi}\cdot100\pi}=200\Omega\)
\(\varphi=\varphi_u-\varphi_i=0-\dfrac{\pi}{4}=-\dfrac{\pi}{4}\)
\(tan\varphi=\dfrac{Z_L-Z_C}{R}\Leftrightarrow tan\dfrac{-\pi}{4}=\dfrac{100-200}{R}\Rightarrow R=100\left(\Omega\right)\)

- Cảm kháng của cuộn dây và dung kháng của tụ điện:
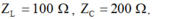
- Biểu diễn phức điện áp hai đầu cuộn cảm:
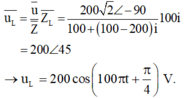
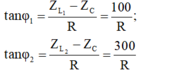
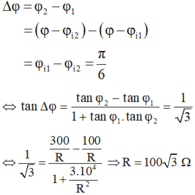
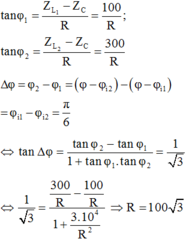

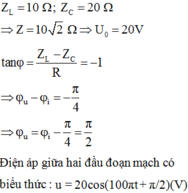
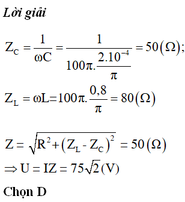
Chọn A
Cảm kháng: ZL = Lω = 30 Ω
Tổng trở: Z= R 2 + Z L 2 = 30 2 Ω
Cường độ dòng điện hiệu dụng: I = I = U Z = 120 30 2 = 4 2 A.
Độ lệch pha: tanφ = Z L R = 1 => φ = π 4 .
Tức là i trễ pha hơn u một góc π 4
Vậy biểu thức tức thời của cường độ dòng điện là: i = 4cos(100πt - π 4 ) (A).