Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

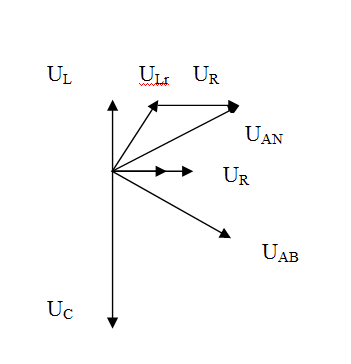
Ta có: \(U_{AB}=U_{AN}=\sqrt{3}U_{MN}=120V\) \(U_R=120V\) \(U_{AB}=U_{AN}\) do đó \(Z_L=U_{LC}\) hay góc hợp giữa \(U_{AB}\) và I bằng góc hợp bởi \(U_{AN}\) và I (cùng có R và r) Mặt khác theo đầu bài của các góc bằng nhau ta suy ra được \(\overrightarrow{U_{AN}}\) là phân giác của góc hợp bởi \(U_{Lr}\) và I \(\overrightarrow{U_{AN}}=\overrightarrow{U_{Lr}}+\overrightarrow{U_R}\) Xét tam giác đã tịnh tiến \(\overrightarrow{U_R}\) lên trên thì theo góc so le của 2 đường song song suy ra đây là tam giác cân \(U_{Lr}=U_R=120V\) Từ đó suy ra góc nhỏ trong tam giác bằng \(\pi\text{ /}6\) Do đó \(U_L=60\sqrt{3}V\) \(Z_L=\frac{U_L}{I}=15\sqrt{6}\Omega\)
|

Chọn D
Tụ xoay có điện dung biến thiên liên tục và tỉ lệ thuận với góc quay theo hàm bậc nhất nên ta có C = a.α + b (pF)
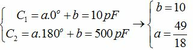
Khi α = 90 o → C = 255 p F
Bước sóng thu được:
![]()

Vì 2 tổng đại số của hiệu điện thể 2 đoạn bằng đúng hiệu điện thế của 2 đầu mạch nên 2 hiệu điện thế này cùng pha với nhau và cùng pha với hiệu điện thế toàn mạch
Do đó ta có
\(\frac{Z_{L_1}}{L_2}=\frac{Z_{L2}}{L_2}\)
Suy ra \(Z_{L_2}=\frac{\omega L_1}{R_1}R_2=50\sqrt{3}\Omega\)
Góc nghiêng so với cường độ dòng là
\(\tan\alpha=\frac{Z_1}{R_1}=\sqrt{3}\) suy ra \(\alpha=\pi\text{/}3\)
Tổng kháng toàn mạch sẽ là
\(Z=\frac{R_1+R_2}{\cos\pi\text{/}3}=300\Omega\)
Biểu thức cường độ dòng sẽ là
\(i=0,5\sqrt{2}\cos\left(100\pi t-\pi\text{/}3\right)A\)
\(Z_L=100\sqrt 3\Omega\)
Vì \(Z_{AB}=Z_{AM}+Z_{MB}\)
Nên \(u_{AM}\) cùng pha với \(u_{MB}\)
\(\Rightarrow \tan\varphi_{AM}=\tan\varphi_{MB}\)
\(\Rightarrow \dfrac{Z_{L1}}{R_1}=\dfrac{Z_{L2}}{R_2}\)
\(\Rightarrow \dfrac{Z_{L1}}{100}=\dfrac{100\sqrt 3}{50}\)
\(\Rightarrow Z_{L1}=200\sqrt 3\Omega\)
Tổng trở \(Z=\sqrt{(100+50)^2+(200\sqrt 3+100\sqrt 3)^2}=150\sqrt{13}\Omega\)
Cường độ dòng điện \(I_0=\dfrac{150\sqrt 2}{150\sqrt {13}}=\sqrt{\dfrac{2}{13}}(A)\)
\(\tan\varphi=2\sqrt 3\)
\(\Rightarrow \varphi = 0,857\) rad
\(\Rightarrow i=\sqrt{\dfrac{2}{13}}\cos(100\pi t-0,857)(A)\)

Đề nghị bạn viết tiếng Việt có dấu nhé, nếu không sẽ không được giúp đỡ đâu.
Khi tụ xoay từ \(0^0 \rightarrow 180 ^0 : \) \(C_1 = 10pF \rightarrow C_2 = 500 pF\)
=> Tụ xoay từ \(0^0 \rightarrow 90^0: \) \(C_1 = 10pF \rightarrow C_x\)
Khi đó ta có: \((180-0) .(C_x-C_1) = (C_2-C_1).(90-0)\)
=> \(C_x-C_1 = \frac{(C_2-C_1)90}{180} = 245pF.\)
=> \(C_x = 255pF.\)
\(\lambda = c.2\pi \sqrt{LC} \approx 134,6m.\)
Chọn đáp án.C