Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
CÁCH 1
Xét phép thử “Bạn lớp trưởng nữ chọn ngẫu nhiên 4 học sinh khác trong lớp”
Khi đó: ![]()
Gọi A là biến cố: “4 học sinh được chọn có cả nam và nữ”.
Ta xét các trường hợp:
TH1: Chọn được 1 nữ, 3 nam. Số cách chọn là: ![]()
TH2: Chọn được 2 nữ, 2 nam. Số cách chọn là: ![]() .
.
TH3: Chọn được 3 nữ, 1 nam. Số cách chọn là: ![]() .
.
Suy ra ![]()
Vậy xác suất cần tìm là: ![]()
CÁCH 2
Xét phép thử “Bạn lớp trưởng nữ chọn ngẫu nhiên 4 học sinh khác trong lớp”
Khi đó: ![]()
Gọi A là biến cố: “4 học sinh được chọn có cả nam và nữ” thì A ¯ là biến cố: “cả 4 học sinh được chọn chỉ có nam hoặc nữ”.
Ta có ![]()
Do đó xác suất xảy ra của biến cố
A
¯
là: 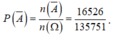
Suy ra ![]()

Chọn C
Gọi A: “4 học sinh được chọn có cả nam và nữ.”
=> A ¯ : “4 học sinh được chọn chỉ có nam hoặc chỉ có nữ.”
Số cách để lớp trưởng nữ chọn ngẫu nhiên 4 học sinh khác: Ω = C 44 4
Số cách chọn 4 học sinh toàn là nam: C 25 4
Số cách chọn 4 học sinh toàn là nữ: C 19 4
Xác suất để 4 học sinh được chọn có cả nam và nữ:
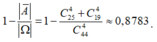

Do yêu cầu xếp xen kẽ nên chỉ có thể xếp theo phương án: người đầu tiên là nam, sau đó xen kẽ nam, nữ và người xếp cuối cùng cũng sẽ là nam.
Số cách xếp 20 bạn nam thành một hàng là 20!. Khi đó giữa các bạn nam có 19 khoảng trống để xếp 19 bạn nữ, có 19! cách xếp các bạn nữ.
Theo quy tắc nhân ta được số cách xếp thỏa mãn là 20!.19!.
Chọn C.

Đáp án C
Phương pháp:
Sử dụng quy tắc nhân
Để chọn được nhóm có một bạn nam và một bạn nữ ta làm như sau:


Khi đó, số cách chọn hai bạn sao cho có một bạn nam và một bạn nữ là:
![]()

Chọn A
Số cách chọn một bạn nam là 12 cách.
Số cách chọn một bạn nữ là 10 cách
Vậy số cách chọn hai bạn trực nhật có cả nam và nữ là 12.10 = 120 (cách)

Đáp án A
Có 2 trường hợp như sau
+)TH1: có 3 nam, 2 nữ, suy ra có C 5 3 C 7 2 = 210 cách chọn
+) TH2: có 4 nam, 1 nữ, suy ra có C 5 4 C 7 1 = 35 cách chọn
Suy ra xác suất cần tính bằng
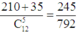

a, Gọi A là biến cố "Cả 3 bạn là nam".
\(\left|\Omega\right|=C^3_{25}\)
\(\left|\Omega_A\right|=C^3_{13}\)
\(\Rightarrow P\left(A\right)=\dfrac{\left|\Omega_A\right|}{\left|\Omega\right|}=\dfrac{C^3_{13}}{C^3_{25}}=\dfrac{143}{1150}\)


Đáp án A
C 20 1 . C 16 1 = 320 cách