Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu: \(C_5^3=10\)
Chọn 3 bạn có ít nhất 2 nữ: ta có 2 trường hợp thuận lợi là 2 nữ 1 nam và 3 bạn đều nữ
\(\Rightarrow C_2^1.C_3^2+C_3^3=7\) cách
Xác suất: \(P=\dfrac{7}{10}\)

Chọn B
Chọn mỗi tổ 2 bạn nên số phần tử của không gian mẫu ![]() .
.
Gọi A là biến cố : “Có đúng 3 bạn nữ trong 4 bạn đi lao động”, khi đó
TH1: Chọn 2 nữ tổ I, 1 nữ tổ II, 1 nam tổ II có ![]() .
.
TH2: Chọn 2 nữ tổ II, 1 nữ tổ I, 1 nam tổ I có ![]() .
.
Suy ra ![]() .
.
Xác suất để chọn 4 bạn đi lao động có đúng 3 bạn nữ là ![]() .
.

\(n\left(\Omega\right)=C^2_8\)
\(n\left(A\right)=C^2_5\)
=>P(A)=5/14

Chọn B.
Không gian mẫu có số phần tử là ![]() .
.
Gọi A là biến cố: “Trong 5 bạn được chọn có cả nam và nữ, đồng thời số nam nhiều hơn số nữ”. Khi đó, số kết quả thuận lợi cho biến cố A là: ![]() .
.
Vậy xác suất cần tính là 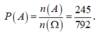 .
.

a.
Xếp 4 bạn nữ cạnh nhau: \(4!\) cách
Coi 4 bạn nữ là 1 bạn, xếp với 6 bạn nam: \(7!\) cách
Theo quy tắc nhân ta có: \(4!.7!\) cách
b.
Xếp 6 bạn nam: \(6!\) cách
6 bạn nam tạo thành 7 khe trống, xếp 4 nữ vào 7 khe trống này: \(C_7^4\) cách
\(\Rightarrow6!.C_7^4\) cách
c. Do có 6 nam và 4 nữ nên ko thể tồn tại cách xếp xen kẽ nam nữ (luôn có ít nhất 2 nam đứng cạnh nhau)
d.
Xếp 4 nữ cạnh nhau: \(4!\) cách
Xếp 6 nam cạnh nhau: \(6!\) cách
Hoán vị nhóm nam và nữ: \(2!\) cách
\(\Rightarrow4!.6!.2!\) cách

Gọi A là biến cố: “5 bạn được chọn có cả nam lẫn nữ mà nam nhiều hơn nữ “
- Số phần tử của không gian mẫu: Ω = C 15 5 .
-Số cách chọn 5 bạn trong đó có 4 nam, 1 nữ là: C 8 4 . C 7 1 .
- Số cách chọn 5 bạn trong đó có 3 nam, 2 nữ là: C 8 3 . C 7 2 .
Số cách chọn 5 bạn được chọn có cả nam lẫn nữ mà nam nhiều hơn nữ là:
n A = C 8 4 . C 7 1 + C 8 3 . C 7 2 = 1666
Xác suất để 5 bạn được chọn có cả nam lẫn nữ mà nam nhiều hơn nữ là:
P A = n A Ω = 1666 C 15 5 = 238 429 .
Chọn đáp án B.

Đáp án A
Có 2 trường hợp như sau
+)TH1: có 3 nam, 2 nữ, suy ra có C 5 3 C 7 2 = 210 cách chọn
+) TH2: có 4 nam, 1 nữ, suy ra có C 5 4 C 7 1 = 35 cách chọn
Suy ra xác suất cần tính bằng
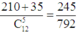

Chọn A
Số cách chọn một bạn nam là 12 cách.
Số cách chọn một bạn nữ là 10 cách
Vậy số cách chọn hai bạn trực nhật có cả nam và nữ là 12.10 = 120 (cách)

Không gian mẫu là chọn ngẫu nhiên 5 học sinh từ 12 học sinh.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 5 học sinh được chọn có 3 học sinh nam và 2 học sinh nữ trong đó phải nhất thiết có bạn An hoặc bạn Hoa nhưng không có cả hai . Ta mô tả các trường hợp thuận lợi cho biến cố A như sau:
● Trường hợp 1. Có bạn An.
Chọn thêm 2 học sinh nam từ 6 học sinh nam, có ![]() cách.
cách.
Chọn 2 học sinh nữ từ 4 học sinh nữ (không chọn Hoa), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
● Trường hợp 2. Có bạn Hoa.
Chọn thêm 1 học sinh nữ từ 4 học sinh nam, có ![]() cách.
cách.
Chọn 3 học sinh nam từ 6 học sinh nam (không chọn An), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
Suy ra số phần tử của biến cố là ![]()
Vậy xác suất cần tính 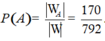
Chọn C.
a, Gọi A là biến cố "Cả 3 bạn là nam".
\(\left|\Omega\right|=C^3_{25}\)
\(\left|\Omega_A\right|=C^3_{13}\)
\(\Rightarrow P\left(A\right)=\dfrac{\left|\Omega_A\right|}{\left|\Omega\right|}=\dfrac{C^3_{13}}{C^3_{25}}=\dfrac{143}{1150}\)
b, Gọi B là biến cố "Có 2 bạn nam và 1 bạn nữ".
\(\left|\Omega\right|=C^3_{25}\)
\(\left|\Omega_B\right|=C^2_{13}.C^1_{12}\)
\(\Rightarrow P\left(B\right)=\dfrac{\left|\Omega_B\right|}{\left|\Omega\right|}=\dfrac{C^2_{13}.C^1_{12}}{C^3_{25}}=\dfrac{234}{575}\)