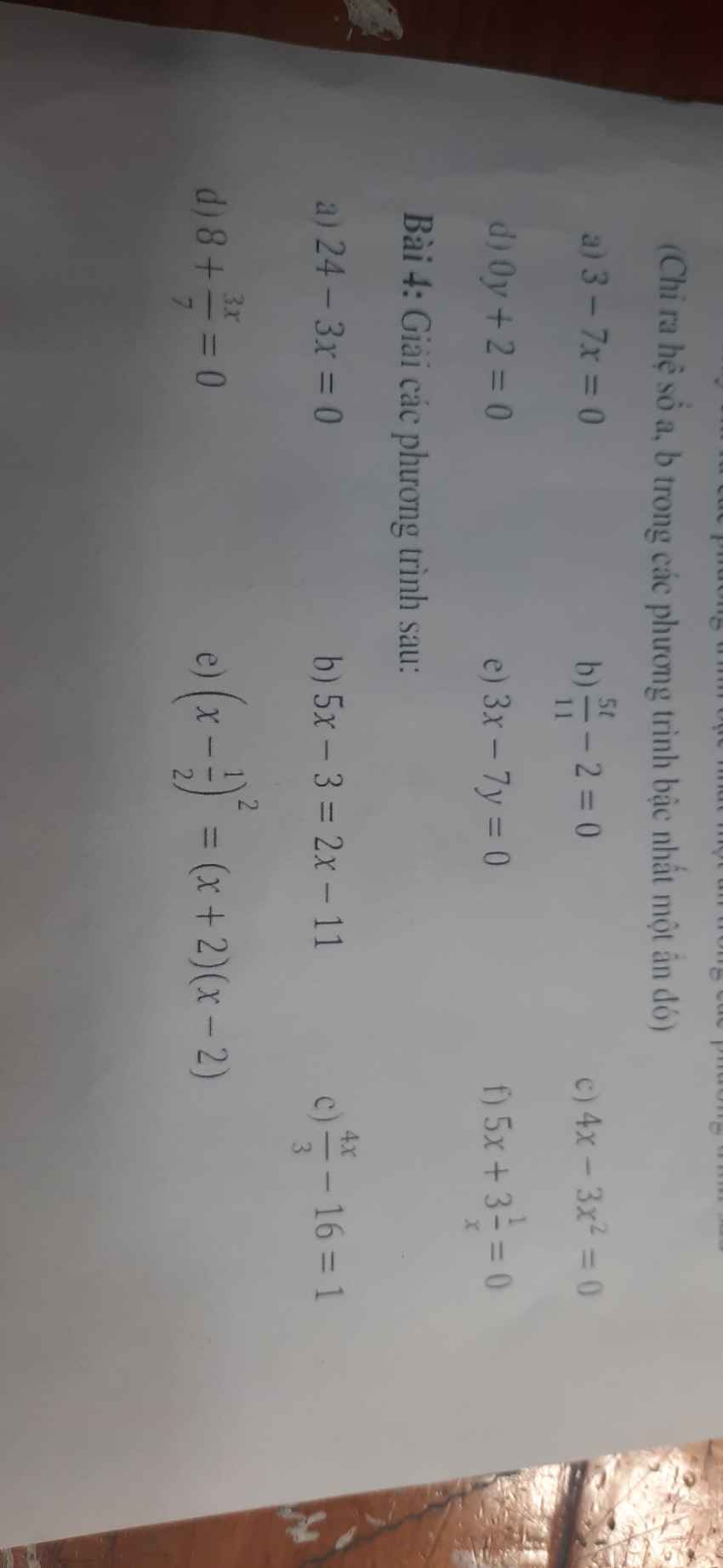Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 3:
Xét ΔBAC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: DE là đường trung bình của ΔBAC
Suy ra: DE//BC và \(DE=\dfrac{BC}{2}\)
Hình thang EDCB có
M là trung điểm của EB
N là trung điểm của DC
Do đó: MN là đường trung bình của hình thang EDCB
Suy ra: MN//ED//BC và \(MN=\dfrac{ED+BC}{2}\)
\(\Leftrightarrow MN=\left(\dfrac{1}{2}BC+BC\right):2=\dfrac{3}{4}BC\)
Xét ΔEBD có
M là trung điểm của EB
MI//ED
Do đó: I là trung điểm của BD
Xét ΔBED có
M là trung điểm của EB
I là trung điểm của BD
Do đó: MI là đường trung bình của ΔBED
Suy ra: \(MI=\dfrac{ED}{2}=\dfrac{1}{4}BC\left(1\right)\)
Xét ΔECD có
N là trung điểm của DC
NK//ED
Do đó: K là trung điểm của EC
Xét ΔECD có
N là trung điểm của DC
K là trung điểm của EC
Do đó: NK là đường trung bình của ΔECD
Suy ra: \(NK=\dfrac{ED}{2}=\dfrac{1}{4}BC\left(2\right)\)
Ta có: MI+IK+KN=MN
nên \(IK=\dfrac{1}{4}BC\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\) suy ra MI=IK=KN


Bài 2:
Gọi K là trung điểm của AD và O là trung điểm của BC
Xét ΔABC có
P là trung điểm của AC
O là trung điểm của BC
Do đó: PO là đường trung bình của ΔABC
Suy ra: PO//AB
hay PO//CD
Xét ΔDAB có
K là trung điểm của AD
Q là trung điểm của BD
Do đó: KQ là đường trung bình của ΔDAB
Suy ra: KQ//AB
hay KQ//CD
Xét ΔBDC có
Q là trung điểm của BD
O là trung điểm của BC
Do đó: QO là đường trung bình của ΔBDC
Suy ra: QO//DC
Ta có: QO//DC
mà PO//DC
và QO,PO có điểm chung là O
nên Q,P,O thẳng hàng
Ta có: KQ//CD
QO//CD
mà KQ và QO có điểm chung là Q
nên K,Q,O thẳng hàng
mà Q,P,O thẳng hàng
nên K,Q,P,O thẳng hàng
hay QP//DC(1)
Xét ΔEAB có
M là trung điểm của EA
N là trung điểm của EB
Do đó: MN là đường trung bình của ΔEAB
Suy ra: MN//AB
hay MN//DC(2)
Từ (1) và (2) suy ra MN//PQ
Xét tứ giác MNPQ có MN//PQ
nên MNPQ là hình thang

Bài 8:
a) Ta có: AD+DB=AB(D nằm giữa A và B)
AE+EC=AC(E nằm giữa A và C)
mà DB=EC(gt)
và AB=AC(ΔABC cân tại A)
nên AD=AE
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
b) Xét ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(AD=AE;AB=AC\right)\)
Do đó: DE//BC(Định lí Ta lét đảo)
c) Xét tứ giác BDEC có DE//BC(cmt)
nên BDEC là hình thang có hai đáy là DE và BC(Định nghĩa hình thang)
Hình thang BDEC(DE//BC) có \(\widehat{B}=\widehat{C}\)(hai góc ở đáy của ΔABC cân tại A)
nên BDEC là hình thang cân(Dấu hiệu nhận biết hình thang cân)
Bài 7:
a) Xét ΔADE vuông tại E và ΔBCF vuông tại F có
AD=BC(ABCD là hình thang cân)
\(\widehat{B}=\widehat{C}\)(ABCD là hình thang cân)
Do đó: ΔADE=ΔBCF(Cạnh huyền-góc nhọn)
Suy ra: DE=CF(Hai cạnh tương ứng)
\(\Leftrightarrow DE+EF=CF+FE\)
\(\Leftrightarrow DF=CE\)
b) Xét tứ giác ABFE có
AE//BF(gt)
AE=BF(ΔAED=ΔBFC)
Do đó: ABFE là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Suy ra: AB=EF(Hai cạnh đối)

\(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-8=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-8\)
Đặt \(x^2+7x=t\)
\(\left(t+10\right)\left(t+12\right)-8=t^2+22t+120-8\)
\(=t^2+22t+112=\left(t+8\right)\left(t+14\right)\)
Theo cách đặt \(=\left(x^2+7x+8\right)\left(x^2+7x+14\right)\)

Bài 1:
Đáp số: 12 kệ thuốc, 10 thùng thuốc
Vì khi cho 2 thùng lên 1 kệ thì thừa 7 kệ(gt)
=> Số kệ >7
Theo công thức: số kệ = thùng : 2+ 7
Vì khi 1 thùng để lên 2 kệ thì thừa 4 thùng (gt)
=> Số thùng >4
Theo công thức: số thùng= thùng : 2 + 4
Từ đó, ta có thể suy ra được đáp số bằng cách rút gọn các số và cách giải cụ thể (hãy hỏi cô giáo)

Bài 4:
a: =>3x=24
hay x=8
b: =>5x-2x=-11+3
=>3x=-8
hay x=-8/3
c: =>4/3x=17
hay x=51/4
d: =>3/7x=-8
hay x=-56/3




 giúp mk với ạ, mk đng cần gấp
giúp mk với ạ, mk đng cần gấp