K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KL
9 tháng 4 2020
Nguyễn Thành Trương ể ể,chữ đẹp vậy.Là một con gái mà thua,nhục và cảm thấy tủi thân quá
10 tháng 11 2023
a: \(\lim\limits_{x\rightarrow3}\dfrac{x^2-9}{x^2-5x+6}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{\left(x-3\right)\left(x+3\right)}{\left(x-3\right)\left(x-2\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{x+3}{x-2}=\dfrac{3+3}{3-2}=\dfrac{6}{1}=6\)
b: \(\lim\limits_{x\rightarrow5}\dfrac{x^2-5x}{x-5}=\lim\limits_{x\rightarrow5}\dfrac{x\left(x-5\right)}{x-5}=\lim\limits_{x\rightarrow5}x=5\)
c: \(\lim\limits_{x\rightarrow-3}\dfrac{x^2-3x}{2x^2+9x+9}\)
\(=\lim\limits_{x\rightarrow-3}\dfrac{x\left(x-3\right)}{2x^2+6x+3x+9}\)
\(=\lim\limits_{x\rightarrow-3}\dfrac{\left(-3\right)\left(-3-3\right)}{\left(-3+3\right)\left(2\cdot\left(-3\right)+3\right)}\)
\(=\lim\limits_{x\rightarrow-3}\dfrac{18}{0\cdot\left(-3\right)}=-\infty\)
HT
23 tháng 2 2021
a/ \(\lim\limits_{x\rightarrow-1}\dfrac{2x^3-5x-4}{\left(x+1\right)^2}=\dfrac{2.\left(-1\right)^3-5\left(-1\right)-4}{\left(-1+1\right)^2}=-\dfrac{1}{0}=-\infty\)
b/ \(\lim\limits\left(x^3+2\sqrt{x^5}-1\right)=\lim\limits x^3\left(1+0-0\right)=+\infty\)
23 tháng 2 2021
giúp em câu này với ạ https://hoc24.vn/hoi-dap/tim-kiem?id=353722985710&q=lim%C2%A0\(\dfrac{1-\dfrac{1}{x}}{1+\dfrac{1}{x}}\)%C2%A0khi+x+ti%E1%BA%BFn+t%E1%BB%9Bi+0
10 tháng 11 2023
a: \(\lim\limits_{x\rightarrow3}\dfrac{\sqrt{2x+10}-4}{3x-9}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{2x+10-16}{3x-9}\cdot\dfrac{1}{\sqrt{2x+10}+4}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{2\left(x-3\right)}{3\left(x-3\right)\cdot\left(\sqrt{2x+10}+4\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{2}{3\left(\sqrt{2x+10}+4\right)}\)
\(=\dfrac{2}{3\cdot\sqrt{6+10}+3\cdot4}=\dfrac{2}{3\cdot4+3\cdot4}=\dfrac{2}{24}=\dfrac{1}{12}\)
b: \(\lim\limits_{x\rightarrow7}\dfrac{\sqrt{4x+8}-6}{x^2-9x+14}\)
\(=\lim\limits_{x\rightarrow7}\dfrac{4x+8-36}{\sqrt{4x+8}+6}\cdot\dfrac{1}{\left(x-2\right)\left(x-7\right)}\)
\(=\lim\limits_{x\rightarrow7}\dfrac{4x-28}{\left(\sqrt{4x+8}+6\right)\cdot\left(x-2\right)\left(x-7\right)}\)
\(=\lim\limits_{x\rightarrow7}\dfrac{4}{\left(\sqrt{4x+8}+6\right)\left(x-2\right)}\)
\(=\dfrac{4}{\left(\sqrt{4\cdot7+8}+6\right)\left(7-2\right)}\)
\(=\dfrac{4}{5\cdot12}=\dfrac{4}{60}=\dfrac{1}{15}\)
c: \(\lim\limits_{x\rightarrow5}\dfrac{x^2-8x+15}{2x^2-9x-5}\)
\(=\lim\limits_{x\rightarrow5}\dfrac{\left(x-3\right)\left(x-5\right)}{2x^2-10x+x-5}\)
\(=\lim\limits_{x\rightarrow5}\dfrac{\left(x-3\right)\left(x-5\right)}{\left(x-5\right)\left(2x+1\right)}\)
\(=\lim\limits_{x\rightarrow5}\dfrac{x-3}{2x+1}=\dfrac{5-3}{2\cdot5+1}=\dfrac{2}{11}\)
27 tháng 3 2023
\(=\lim\limits_{x\rightarrow+\infty}\left(\sqrt{9x^2-2x+3}-3x^2\right)\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{9x^2-2x+3-3x^4}{3x^2+\sqrt{9x^2-2x+3}}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{-3x^4+9x^2-2x+3}{3x^2+\sqrt{9x^2-2x+3}}\)
\(=\lim\limits_{x\rightarrow+\infty}x^2\dfrac{-3+\dfrac{9}{x^2}-\dfrac{2}{x^3}+\dfrac{3}{x^4}}{3+\sqrt{\dfrac{9}{x}-\dfrac{2}{x^2}+\dfrac{3}{x^2}}}=-\infty\)
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{9x + 1}}{{3x - 4}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\left( {9 + \frac{1}{x}} \right)}}{{x\left( {3 - \frac{4}{x}} \right)}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{9 + \frac{1}{x}}}{{3 - \frac{4}{x}}} = \frac{{9 + 0}}{{3 - 0}} = 3\)
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{7x - 11}}{{2x + 3}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{x\left( {7 - \frac{{11}}{x}} \right)}}{{x\left( {2 + \frac{3}{x}} \right)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{7 - \frac{{11}}{x}}}{{2 + \frac{3}{x}}} = \frac{{7 - 0}}{{2 + 0}} = \frac{7}{2}\)
c) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 1} }}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\sqrt {1 + \frac{1}{{{x^2}}}} }}{x} = \mathop {\lim }\limits_{x \to + \infty } \sqrt {1 + \frac{1}{{{x^2}}}} = \sqrt {1 + 0} = 1\)
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
d) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} + 1} }}{x} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - x\sqrt {1 + \frac{1}{{{x^2}}}} }}{x} = \mathop {\lim }\limits_{x \to - \infty } - \sqrt {1 + \frac{1}{{{x^2}}}} = - \sqrt {1 + 0} = - 1\)
e) Ta có: \(\left\{ \begin{array}{l}1 > 0\\x - 6 < 0,x \to {6^ - }\end{array} \right.\)
Do đó, \(\mathop {\lim }\limits_{x \to {6^ - }} \frac{1}{{x - 6}} = - \infty \)
g) Ta có: \(\left\{ \begin{array}{l}1 > 0\\x + 7 > 0,x \to {7^ + }\end{array} \right.\)
Do đó, \(\mathop {\lim }\limits_{x \to {7^ + }} \frac{1}{{x - 7}} = + \infty \)
HT
18 tháng 4 2021
1/ \(=\lim\limits_{x\rightarrow-\infty}x\left(-\sqrt{\dfrac{16x^2}{x^2}-\dfrac{3x}{x^2}+\dfrac{5}{x^2}}+2-\dfrac{5}{x}\right)=\lim\limits_{x\rightarrow-\infty}x\left(-4+2\right)=-\infty\)
\(=\lim\limits_{x\rightarrow+\infty}x\left(\sqrt{\dfrac{16x^2}{x^2}-\dfrac{3x}{x^2}+\dfrac{5}{x^2}}+2-\dfrac{5}{x}\right)=\lim\limits_{x\rightarrow+\infty}x\left(4+2\right)=+\infty\)
2/ \(S=\dfrac{-\dfrac{1}{3}}{1+\dfrac{1}{3}}=-\dfrac{1}{4}\)
4/ 
5/ 
HT
18 tháng 4 2021
\(f'\left(x\right)=4\left(2m-1\right)x^3-4x\)
Vì tiếp tuyến vuông góc với \(y=5x-2018\Rightarrow f'\left(x\right)=-\dfrac{1}{5}\)
\(\Rightarrow f'\left(1\right)=-\dfrac{1}{5}\Leftrightarrow4\left(2m-1\right)-4=-\dfrac{1}{5}\Leftrightarrow m=\dfrac{39}{40}\)
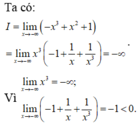
\(\lim\limits_{x\rightarrow3}\dfrac{x^3+2x^2+3x-9}{x^2-9}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{x^3-3x^2+5x^2-15x+18x-54+45}{\left(x-3\right)\left(x+3\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{\left(x-3\right)\left(x^2+5x+18\right)+45}{\left(x-3\right)\left(x+3\right)}\)
\(=+\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow3}\left(x-3\right)\left(x+3\right)=\left(3-3\right)\left(3+3\right)=0\\\lim\limits_{x\rightarrow3}x^3+2x^2+3x-9=3^3+2\cdot3^2+3\cdot3-9=27+2\cdot18=45>0\end{matrix}\right.\)
Sai.