
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

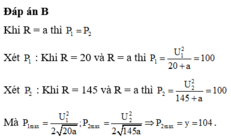

Với đồ thị P 1 , ta thấy rằng:
x và 20 Ω là hai giá trị cho cùng công suất tiêu thụ trên mạch là 100W, 125 W là giá trị cực đại của công suất khi R biến thiên, ta có:
x + 20 = U 1 2 100 125 = U 1 2 2 20 x ⇒ 125 = 100 20 + x 2 20 x ⇒ x = 80 Ω
(lưu ý rằng 20 ≤ x ≤ 145 )
Với đồ thị P 2 , ta thấy rằng:
x và 145 Ω là hai giá trị cho cùng công suất tiêu thụ trên mạch là 100 W, y là giá trị cực đại của P 2 , từ đó ta có: x + 145 = U 2 2 100 y = U 2 2 2 145 x ⇒ y = 100 x + 145 2 145 x ≈ 104 W
Đáp án B

Chọn B.
Hai đồ thị giao nhau tại R =a khi đó P 1 = P 2
Tại R = 20 Ω và R = a có cùng công suất nên:
20. a = R l o = Z L − Z C ⇒ P 1 = U 1 2 .20 20 2 + Z L − Z C 2 = U 1 2 20 + a = 100
R = a và R = 145 Ω có cùng công suất nên tương tự ⇒ P 2 = U 2 2 1245 + a = 100 (2)
Mà
P 1 max = U 1 2 2 Z L − Z C = U 1 2 2 20 a = 125 (3); P 2 max = U 2 2 2 145 a (4)
Từ (1) và (2) suy ra a = 80 , U 1 = 100 V
Thay vào (2) suy ra U 2 = 150 V
Thay vào (4) suy ra P 2 max = U 2 2 2 145 a

Với đồ thị P 1 , ta thấy
x là giá trị cực đại của P 1 , 100 và y là hai giá trị của điện trở cho cùng công suất tiêu thụ trên mạch là 50 W, ta có: 100 + y = U 1 2 50 R 01 2 = 100 y ⇒ 100 + y = 4 , 5 a 2 50 1 x = U 1 2 2 100 y = 50 100 + y 2 100 y 2
Với đồ thị P 2 , ta thấy:
y chính là giá trị để P 2 cực đại bằng 50 W, vậy
P 2 m a x = 50 = U 2 2 2 y ⇔ 50 = 3 a 2 y 3 → 1 & 3 y = 200 Ω ⇒ x = 37 , 5 2 W
Đáp án A

Đặt X = Z L − Z C
Công suất tiêu thụ P 2
P 2 = U 2 R R 2 + X 2 2 với R 02 = 400 Ω ⇒ X 2 = 400 Ω
Công suất tiêu thụ P 1 :
P 1 = U 2 R R 2 + X 1 2 với P 1 R = 100 = P 2 m a x ⇔ U 2 100 100 2 + X 1 2 = U 2 2.400 = 50 ⇒ X 1 2 = 70000 U 2 = 40000
P 1 m a x = U 2 2 X 1 = 40000 2 70000 ≈ 76 W
Đáp án D

Từ giả thuyết bài toán, ta có:
P 1 m a x P 2 m a x = U 1 2 R 2 U 2 2 R 3 = 3 2 ⇔ U 1 2 U 2 2 = 3 R 3 2 R 2 1
Từ đồ thị ta thấy rằng
P 2 m a x = P 1 R 1 ⇔ U 2 2 2 R 2 = U 1 2 R 1 R 1 2 + R 3 2 ⇒ U 1 2 U 2 2 = R 1 2 + R 3 2 2 R 1 R 2 2
Từ (1) và (2) ta thu được R 1 2 + R 3 2 R 1 = 3 R 3 , chuẩn hóa R 1 = 1 ⇒ R 3 2 − 3 R 3 + 1 = 0 ⇒ R 3 = 2 , 6 R 3 = 0 , 4
Vì R 3 > R 1 = 1 ⇒ R 3 = 2 , 6 ⇒ R 2 = 1 , 8
Thay vào (1) ta tìm được U 2 U 1 ≈ 0.68
Đáp án D

Đáp án C
Điều chỉnh L: URmax, UCmax
⇒ Z L = Z C , U R m a x = U 1 = U ; U c m a x = U 3 = U . Z C R U L m a x
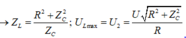
Theo đề:
U 2 = 2 . U 1 ⇒ U R 2 + Z 2 C R = 2 . U → Z C = R 3 ⇒ U 3 = U 3 = 80 3 ( V )

- Từ đồ thị ta thấy có hai giá trị của ZL là 60Ω và 140Ω cùng cho 1 giá trị P.
- Vị trí P3 đạt cực đại ứng với trường hợp cộng hưởng điện ZL = ZC
- Và có mối quan hệ giữa ZL3 với ZL1 và ZL2 là:
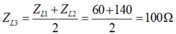
- Khi ZL = 0 thì mạch có công suất P1 thỏa mãn P3 /P1 = 3. Ta có:
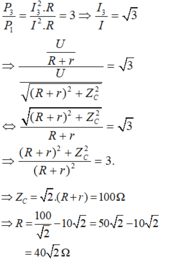

Giải thích: Đáp án B
Từ đồ thị ta có:
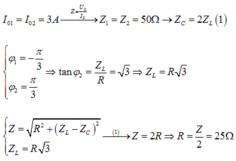
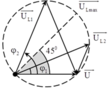
Cách 2: Dùng giản đồ vectơ kép
Từ đồ thị ta có tại thời điểm t = 0 hai dao động đường (1) và (2) được biễu diễn trên VTLG như sau:
Từ VTLG suy ra dòng điện trong hai trường hợp lệch pha nhau 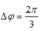
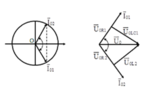
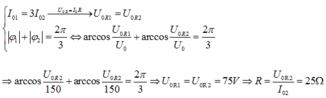

Hệ số công suất của mạch khi xảy ra cực đại điện áp trên cuộn cảm.
P = 0 , 5 P m a x = P m a x cos 2 φ 0 ⇒ φ 0 = 45 0
→ góc hợp bởi U L m a x → và U → là 45 độ .
Biểu diễn điện áp trên đoạn mạch bằng các vecto. Ta để ý rằng U 1 = U 2 → U L 1 → và U L 2 → nằm đối xứng nhau qua đường kính của đường tròn.
Từ hình vẽ ta có: φ 2 + φ 1 = 90 0 φ 2 = φ 1 + 60 0 ⇒ φ 1 = 15 0
Đáp án B