
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1,\\ a,=\dfrac{\sqrt{\left(\sqrt{a}-\sqrt{b}\right)^2}}{\sqrt{\left(\sqrt{a}-\sqrt{b}\right)}}=\sqrt{\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2}{\sqrt{a}-\sqrt{b}}}=\sqrt{\sqrt{a}-\sqrt{b}}\\ b,=\dfrac{\sqrt{\left(\sqrt{x}-\sqrt{3}\right)\left(\sqrt{x}+\sqrt{3}\right)}}{\sqrt{\sqrt{x}+\sqrt{3}}}\cdot\dfrac{\sqrt{3}}{\sqrt{\sqrt{x}-\sqrt{3}}}\\ =\sqrt{3}\\ c,=2y^2\cdot\dfrac{x^2}{\left|2y\right|}=\dfrac{2x^2y^2}{-2y}=-x^2y\\ d,=5xy\cdot\dfrac{\left|5x\right|}{y^2}=\dfrac{-25x^2y}{y^2}=\dfrac{-25x^2}{y}\)
Bài 2:
a: Ta có: \(A=\left(3\sqrt{18}+2\sqrt{50}-4\sqrt{72}\right):8\sqrt{2}\)
\(=\left(9\sqrt{2}+10\sqrt{2}-24\sqrt{2}\right):8\sqrt{2}\)
\(=\dfrac{-5\sqrt{2}}{8\sqrt{2}}=-\dfrac{5}{8}\)
b: Ta có: \(B=\left(-4\sqrt{20}+5\sqrt{500}-3\sqrt{45}\right):\sqrt{5}\)
\(=\left(-8\sqrt{5}+50\sqrt{5}-9\sqrt{5}\right):\sqrt{5}\)
\(=49\)

Bài 3:
1: Ta có: \(P=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}-\dfrac{5\sqrt{x}+2}{x-4}\)
\(=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)

\(1+\sqrt{3x+1}=3x\)
⇔ \(\sqrt{3x+1}=3x-1\)
ĐKXĐ : x ≥ 1/3
Bình phương hai vế
⇔ 3x + 1 = 9x2 - 6x + 1
⇔ 9x2 - 6x + 1 - 3x - 1 = 0
⇔ 9x2 - 9x = 0
⇔ 9x( x - 1 ) = 0
⇔ 9x = 0 hoặc x - 1 = 0
⇔ x = 0 ( ktm ) hoặc x = 1 ( tm )
Vậy x = 1
\(1+\sqrt{3x+1}=3x\left(ĐKXĐ:x\ge-\frac{1}{3}\right)\)
\(\sqrt{3x+1}=3x-1\)
\(\left(\sqrt{3x+1}\right)^2=\left(3x-1\right)^2\)
\(3x+1=9x^2-6x+1\)
\(9x^2-9x=0\)
\(9x\left(x-1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}9x=0\\x-1=0\end{cases}\Rightarrow}\orbr{\begin{cases}x=0\\x=1\end{cases}}\)

Vd1:
d) Ta có: \(\sqrt{2}\left(x-1\right)-\sqrt{50}=0\)
\(\Leftrightarrow\sqrt{2}\left(x-1-5\right)=0\)
\(\Leftrightarrow x=6\)


a: góc ASB=1/2*180=90 độ=góc ABM
b: ON vuông góc AS
BS vuông góc SA
=>ON//BS
c: góc OIM+góc OBM=180 độ
=>OIMB nội tiếp


\(M=\left(\dfrac{\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\right).\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{2\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{2\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
2. Ta có:
\(\sqrt{x}>0\Rightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}+2}>0\) hay \(M>0\)
Lại có: \(M=\dfrac{\sqrt{x}+2-1}{\sqrt{x}+2}=1-\dfrac{1}{\sqrt{x}+2}< 1\)
\(\Rightarrow0< M< 1\Rightarrow M>M^2\)
1) Ta có: \(M=\left(\dfrac{\sqrt{x}}{x-4}+\dfrac{1}{\sqrt{x}-2}\right)\cdot\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{\sqrt{x}+\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{2\sqrt{x}+2}{2\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)







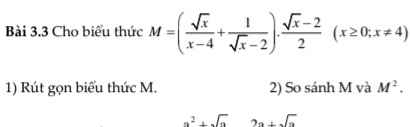
a) Để y là hsbn thì \(2-m\ne0\Leftrightarrow m\ne2\)
b) Để y là hsnb thì \(2-m< 0\Leftrightarrow m>2\)
Để y là hsđb thì \(2-m>0\Leftrightarrow m< 2\)
c) Vì đths \(\left(d\right):y=\left(2-m\right)x+m-1\)đi qua A(2;1) nên ta thay x = 2; y = 1 vào phương trình đường thẳng (d), ta có:
\(1=2\left(2-m\right)+m-1\Leftrightarrow1=4-2m+m-1\Leftrightarrow2m-m-3=-1\Leftrightarrow m=2\)
Vậy để đths \(\left(d\right):y=\left(2-m\right)x+m-1\)đi qua điểm A(2;1) thì m = 2
d) Gọi điểm cố định mà đths \(\left(d\right):y=\left(2-m\right)x+m-2\)luôn đi qua với mọi m là B(x0;y0)
Thay x = x0; y = y0 vào phương trình đường thẳng (d), ta có:
\(y_0=\left(2-m\right)x_0+m-2\)\(\Leftrightarrow\)\(y_0=2x_0-mx_0+m-1\)\(\Leftrightarrow\)\(mx_0-m-2x_0+y_0+1=0\)
\(\Leftrightarrow m\left(x_0-1\right)-\left(2x_0-y_0-1\right)=0\)(*)
Vì phương trình (*) luôn phải có nghiệm đúng với mọi m nên (*) \(\Leftrightarrow\hept{\begin{cases}x_0-1=0\\2x_0-y_0-1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x_0=1\\2.1-y_0=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x_0=1\\y_0=1\end{cases}}\)
Vậy B(1;1) là điểm cố định mà đths \(y=\left(2-m\right)x+m-1\)luôn đi qua với mọi m.
Câu 2 bạn tự vẽ được mà.