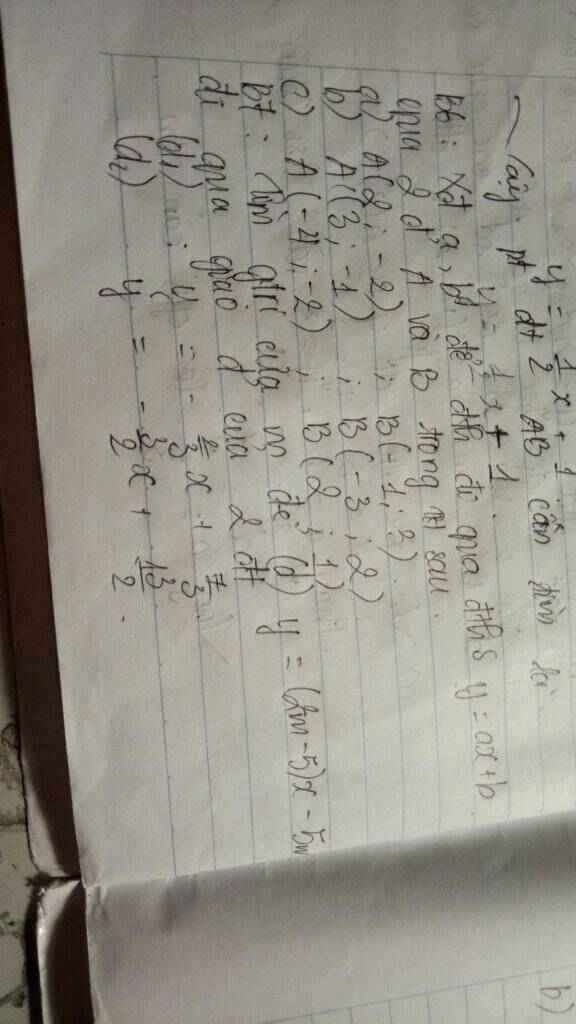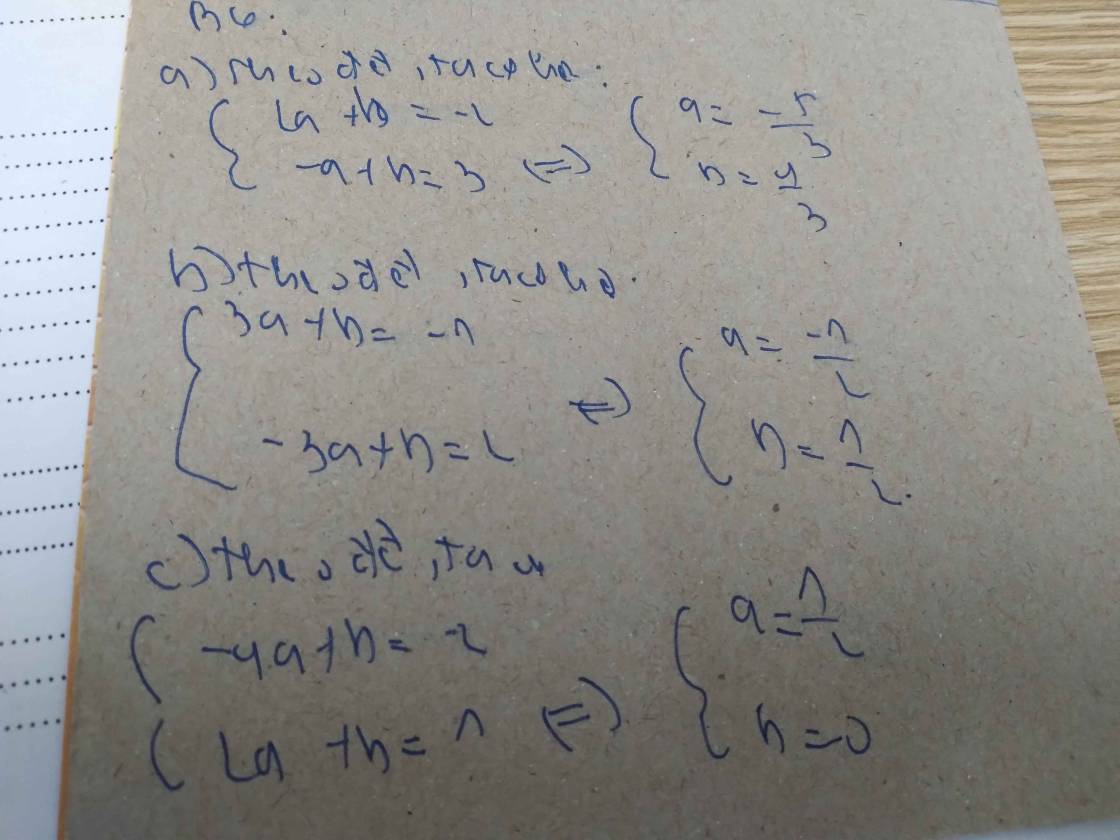K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5 tháng 6 2021
5)Áp dụng BĐT bunhia ta có:
`P^2<=(1+1+1)(x+y+y+z+z+x)`
`<=>P^2<=3.2(x+y+z)=6`
Mà `P>=0`
`=>P<=sqrt6`
Dấu "=" `<=>x=y=z=1/3`
5 tháng 6 2021
1c của bạn đấy @@
`1c)P=A.B`
`=(sqrtx-1)/(sqrtx+3)*(sqrtx+3)/(sqrtx-3)`
`=(sqrtx-1)/(sqrtx-3)`
`|P|+P=0`
`<=>|P|=-P`
`<=>P<=0`
`<=>(sqrtx-1)/(sqrtx-3)<=0`
Vì `sqrtx-1>sqrtx-3`
`=>` $\begin{cases}\sqrt{x}-1 \ge 0\\\sqrt{x}-3 <0\end{cases}$
`<=>` $\begin{cases}\sqrt{x} \ge 1\\\sqrt{x}<3\end{cases}$
`<=>` $\begin{cases}x \ge 1\\x<9\end{cases}$
`<=>1<=x<9`
Vậy `1<=x<9` thì....
10 tháng 9 2023
6: ĐKXĐ: y<>0; y<>2; y<>-2; y<>3
a: \(P=\left(\dfrac{-\left(y+2\right)}{y-2}-\dfrac{4y^2}{\left(y-2\right)\left(y+2\right)}+\dfrac{y-2}{y+2}\right):\dfrac{y\left(y-3\right)}{y^2\left(2-y\right)}:\dfrac{1}{y-3}\)
\(=\dfrac{-y^2-4y-4-4y^2+y^2-4y+4}{\left(y-2\right)\left(y+2\right)}\cdot\dfrac{y\left(2-y\right)}{y-3}\cdot\dfrac{y-3}{1}\)
\(=\dfrac{-4y^2-8y}{\left(y-2\right)\left(y+2\right)}\cdot\dfrac{-y\left(y-2\right)}{1}\)
\(=4y^2\)
b: 2y^2-3y-2=0
=>2y^2-4y+y-2=0
=>(y-2)*(2y+1)=0
=>y=2(loại) hoặc y=-1/2(nhận)
Khi y=-1/2 thì P=4*(-1/2)^2=1
6 tháng 8 2023
4:
a: Xét ΔCAB vuông tại C có CH là đường cao
nên CH^2=HA*HB
=>CH=căn 2*8=4cm
Xét ΔACB vuông tại C có CH là đường cao
nên CA^2=CH*CB và CB^2=BH*BA
=>CA^2=2*10=20 và CB^2=8*10=80
=>CA=2căn 5(cm) và CB=4căn 5(cm)
b: Xét tứ giác CMHN có
góc CMH+góc CNH=180 độ
=>CMHN là tứ giác nội tiếp
=>C,M,H,N cùng thuộc 1 đường tròn
2 tháng 7 2023
a: \(P=\dfrac{a+1+\sqrt{a}}{a+1}:\dfrac{a+1-2\sqrt{a}}{\left(\sqrt{a}-1\right)\left(a+1\right)}\)
\(=\dfrac{a+\sqrt{a}+1}{a+1}\cdot\dfrac{\left(a+1\right)\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-1\right)^2}=\dfrac{a+\sqrt{a}+1}{\sqrt{a}-1}\)
b: P<1
=>P-1<0
=>\(\dfrac{a+\sqrt{a}+1-\sqrt{a}+1}{\sqrt{a}-1}< 0\)
=>căn a-1<0
=>0<a<1
c: Thay x=19-8căn3 vào P, ta được:
\(P=\dfrac{19-8\sqrt{3}+4+\sqrt{3}+1}{4+\sqrt{3}-1}=\dfrac{31-15\sqrt{3}}{2}\)
5 tháng 12 2021
a) d cắt d' ⇒ a≠a'
\(\Leftrightarrow k-3\ne2k+1\Leftrightarrow k\ne-4\)
b) d // d' ⇒ a=a'
\(\Leftrightarrow k-3=2k+1\Leftrightarrow k=-4\)
c) d cắt d' 1 điểm trên trục tung ⇒ a≠a' và b=b'
\(\Leftrightarrow\left\{{}\begin{matrix}k-3\ne2k+1\\-3k+4=k+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}k\ne-4\\k=-\dfrac{1}{4}\end{matrix}\right.\)
29 tháng 7 2021
Vd1:
d) Ta có: \(\sqrt{2}\left(x-1\right)-\sqrt{50}=0\)
\(\Leftrightarrow\sqrt{2}\left(x-1-5\right)=0\)
\(\Leftrightarrow x=6\)