
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


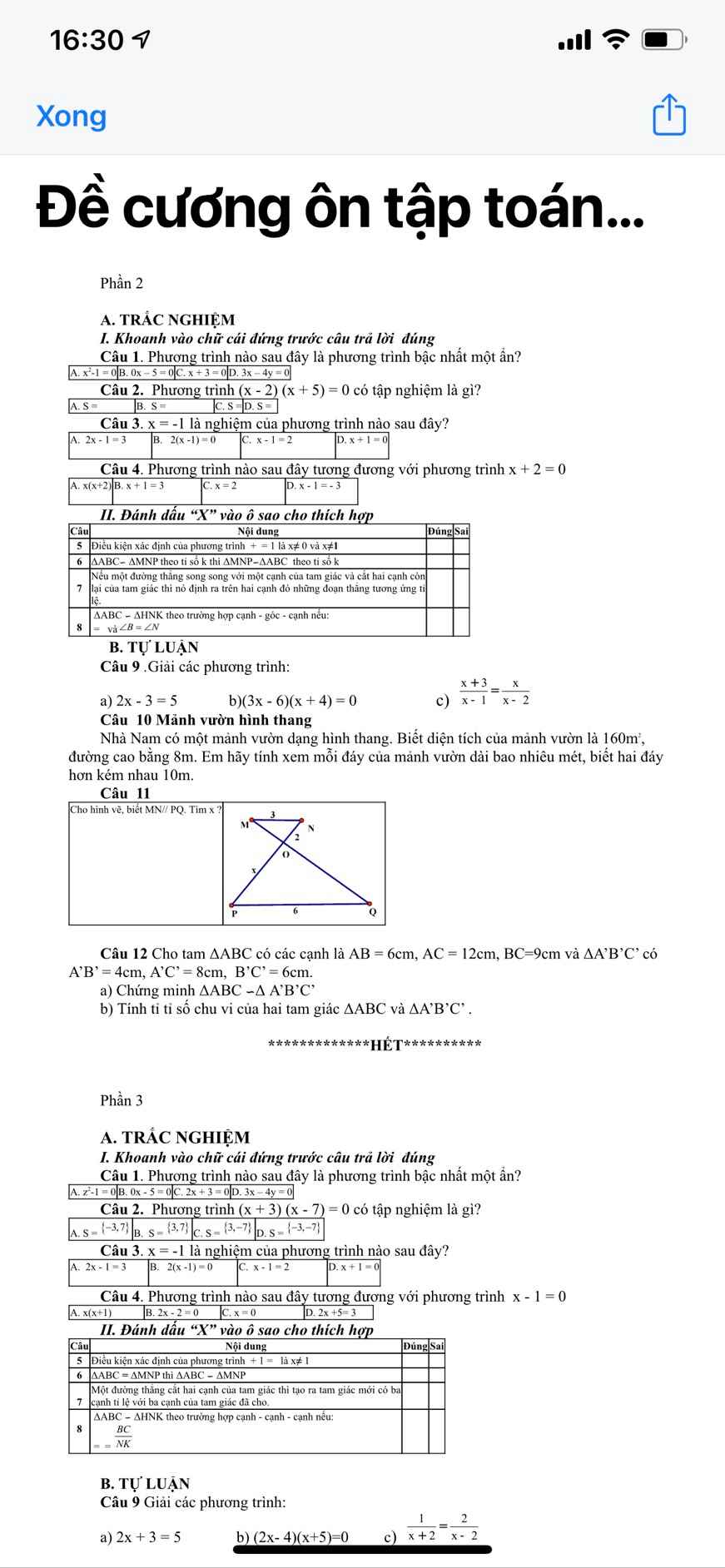
Câu 9:
a: 2x+3=5
nên 2x=2
hay x=1
b: (2x-4)(x+5)=0
=>(x-2)(x+5)=0
=>x-2=0 hoặc x+5=0
=>x=2 hoặc x=-5
c: 1/x+2=2/x-2
=>2x+4=x-2
=>x=-6

Bài 3:
\(b,\Leftrightarrow\left(x+8\right)\left(x+8-3x\right)=0\\ \Leftrightarrow\left(x+8\right)\left(8-2x\right)=0\\ \Leftrightarrow2\left(4-x\right)\left(x+8\right)=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-8\end{matrix}\right.\)

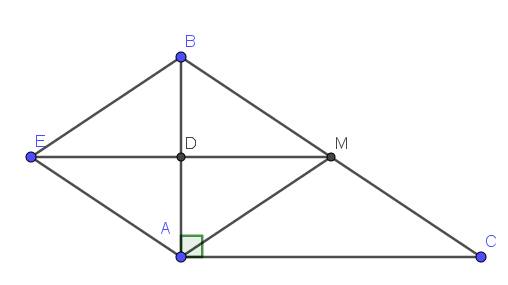
a: Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
nên ADHE là hình chữ nhật
Suy ra: AH=DE
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
c: Xét ΔAHB vuông tại H có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
hay AD/AC=AE/AB
Xét ΔADE vuông tại A và ΔACB vuông tại A có
AD/AC=AE/AB
Do đó: ΔADE\(\sim\)ΔACB


\(8,=\left(2x-3\right)\left(2x+3\right)\\ 9,=\left(1-5a^2\right)\left(1+5a^2\right)\)
8) \(-9+4x^2=\left(2x\right)^2-3^2=\left(2x-3\right)\left(2x+3\right)\)
9) \(1-25a^4=1-\left(5a^2\right)^2=\left(1-5a^2\right)\left(1+5a^2\right)\)

a.
Ta có \(BD||AC\) (cùng vuông góc AB)
Áp dụng định lý Talet trong tam giác ACE: \(\dfrac{BE}{BA}=\dfrac{DE}{DC}\)
b.
Ta có \(IK||BD||AC\) \(\Rightarrow EI||AC\)
Áp dụng Talet: \(\dfrac{DC}{ED}=\dfrac{DA}{ID}\Rightarrow\dfrac{DC}{DC+ED}=\dfrac{DA}{DA+ID}\Rightarrow\dfrac{DC}{CE}=\dfrac{DA}{AI}\) (1)
Do \(BD||EK\), áp dụng Talet trong tam giác CEK: \(\dfrac{BD}{EK}=\dfrac{CD}{CE}\) (2)
Do \(BD||EI\), áp dụng Talet trong tam giác AEI: \(\dfrac{BD}{EI}=\dfrac{AD}{AI}\) (3)
Từ(1);(2);(3) \(\Rightarrow\dfrac{BD}{EK}=\dfrac{BD}{EI}\Rightarrow EK=EI\)

1. x2-x-2
=(x2-2x)+(x-2)
= x(x-2)+(x-2)
= (x+1)(x-2)
2.x2-3x+2
=x2-x-2x+2
=(x2-x)-(2x-2)
=x(x-1)-2(x-1)
=(x-2)(x-1)
3.-x2-2x+3
=3-2x-x2
=3+x-3x-x2
=(3+x)-(3x+x2)
=(3+x)-x(3+x)
=(1-x)(3+x)
4. x2-5x+4
=x2-x-4x+4
=(x2-x)-(4x-4)
=x(x-1)-4(x-1)
=(x-1)(x-4)
5. x2-5x+6
=x2-2x-3x+6
=(x2-2x)-(3x-6)
=x(x-2)-3(x-2)
=(x-2)(x-3)
6.x2-6x+5
=(x2-x)-(5x-5)
=x(x-1)-5(x-1)
=(x-1)(x-5)
7.x2-7x+12
=(x2-3x)-(4x-12)
=x(x-3)-4(x-3)
=(x-4)(x-3)
8.-x2+7x-12
=(-x2+3x)+(4x-12)
=-x(x-3)+4(x-3)
=(4-x)(x-3)
9.x2-3x-4
=(x2+x)-(4x+4)
=x(x+1)-4(x+1)
=(x-4)(x+1)
mik làm 1 nửa thôi dài quá

\(5,\Leftrightarrow8\left(x^2-5x+3x-15\right)-\left(8x^2-4x+20x-10\right)=0\)
\(\Leftrightarrow8x^2-40x+24x-120-8x^2+4x-20x+10=0\)
\(\Leftrightarrow-32x-110=0\)
\(\Leftrightarrow x=\dfrac{110}{-32}=-\dfrac{55}{16}\)
\(9,\Leftrightarrow\left(5x-5\right)\left(2x+7-2x-1\right)=x+2-x+5\)
\(\Leftrightarrow6\left(5x-5\right)=7\)
\(\Leftrightarrow5x-5=\dfrac{7}{6}\)
\(\Leftrightarrow x=\dfrac{37}{30}\)
\(8,\Leftrightarrow\left(6x-3\right)\left(x-5-3x+1\right)-3+13=0\)
\(\Leftrightarrow-6\left(2x-1\right)\left(x+2\right)+10=0\)
\(\Leftrightarrow2x^2-x+4x-2=\dfrac{10}{6}\)
\(\Leftrightarrow2x^2+3x-\dfrac{11}{3}=0\)
\(10,\Leftrightarrow8x\left(x^2+x+6x+6\right)-8x^3=5x\)
\(\Leftrightarrow8x^3+8x^2+48x^2+48x-8x^3-5x=0\)
\(\Leftrightarrow56x^2+43x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{43}{56}\end{matrix}\right.\)
Vậy ....
;-; quên đọc đề may làm trúng 9; 10 câu 6 nốt đây nha
\(6,\Leftrightarrow9x^2-9x-8x^2+40-x^2=5x-3-7x+4\)
\(\Leftrightarrow9x^2-9x-8x^2+40-x^2-5x+3+7x-4=0\)
\(\Leftrightarrow-7x+39=0\)
\(\Leftrightarrow x=\dfrac{39}{7}\)
Vậy ...


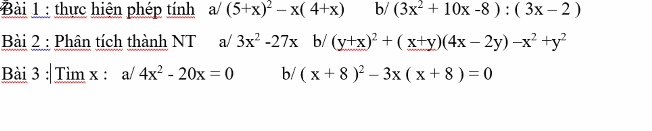








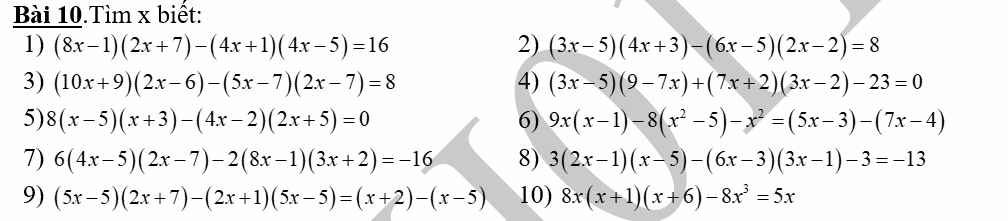 giúp em câu 6,9,10 câu này khó em k làm dc
giúp em câu 6,9,10 câu này khó em k làm dc
Lời giải:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (cm)
Dễ thấy $DM$ là đường trung bình của tam giác ABC ứng với cạnh $AC$
$\Rightarrow DM\parallel AC$
$\Rightarrow DM\perp AB$
Tam giác $MBD$ và $MAD$ có:
$BD=DA$
$\widehat{MDB}=\widehat{MDA}=90^0$
$DM$ chung
$\Rightarrow \triangle MBD=\triangle MAD$ (c.g.c)
$\Rightarrow MA=MB=\frac{BC}{2}=10:2=5$ (cm)
c.
Tứ giác $AEBM$ có 2 đường chéo $AB, EM$ cắt nhau tại trung điểm $D$ của mỗi đường nên $AEBM$ là hình bình hành.
Mà $AB\perp EM$ ở $D$ (suy ra từ việc cm $MD\perp AB$)
$\Rightarrow AEBM$ là hình thoi.
c.
Để $AEBM$ là hình vuông thì $\widehat{AMB}=90^0$
$\Leftrightarrow AM\perp BC$
$\Leftrightarrow$ trung tuyến $AM$ đồng thời là đường cao
$\Leftrightarrow \triangle ABC$ cân tại $A$
Hình vẽ: