
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: góc CAO+góc CMO=180 độ
=>CAOM nội tiếp
b: Xét (O) có
CA,CM là tiếp tuyến
=>CA=CM và OC là phân giác của góc MOA(1)
Xét (O) co
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
CD=CM+MD=CA+DB
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
c: AC*BD=CM*MD=OM^2=R^2

a: Δ=(m-2)^2-4(m-4)
=m^2-4m+4-4m+16
=m^2-8m+20
=m^2-8m+16+4
=(m-2)^2+4>=4>0
=>Phương trình luôn có 2 nghiệm pb
b: x1^2+x2^2
=(x1+x2)^2-2x1x2
=(m-2)^2-2(m-4)
=m^2-4m+4-2m+8
=m^2-6m+12
=(m-3)^2+3>=3
Dấu = xảy ra khi m=3

a: Khi m=-2 thì (1) sẽ là x^2+2x-8=0
=>x=-4 hoặc x=2
b: Δ=(2m+2)^2-4(2m-4)
=4m^2+8m+4-8m+16
=4m^2+20>0 với mọi m
=>Phương trình luôn có hai nghiệm phân biệt
c: A=x1^2+x2^2=(x1+x2)^2-2x1x2
=(2m+2)^2-2(2m-4)
=4m^2+8m+4-4m+8
=4m^2+4m+12=(2m+1)^2+11
d: A>=11
Dấu = xảy ra khi m=-1/2

Gọi chiều dài và chiều rộng lần lượt là a,b
Theo đề, ta có; a+b=170 và 3a-4b=20
=>a=100 và b=70
Diện tích là 100*70=7000m2

a: Khi m=2 thì pt se là 2x^2-5x+3=0
=>(x-1)(2x-3)=0
=>x=1 hoặc x=3/2
b: Khi x=-1 thì hệ sẽ là 2*(-1)^2+1(m+3)+3=0
=>m+6+2=0
=>m=-8
x1*x2=3/2
=>x2=-3/2

Lời giải:
a. Với $m=0$ thì pt trở thành:
$x^2+x=0$
$\Leftrightarrow x(x+1)=0$
$\Leftrightarrow x=0$ hoặc $x+1=0$
$\Leftrightarrow x=0$ hoặc $x=-1$
b. Ta thấy: $\Delta=(m+1)^2-4m=(m-1)^2\geq 0, \forall m\in\mathbb{R}$ nên pt luôn có nghiệm với mọi $m$
c.
Áp dụng định lý Viet ta có:
$x_1+x_2=-(m+1)$
$x_1x_2=m$
Khi đó:
$x_1^2+x_2^2=(x_1+x_2)^2-2x_1x_2=(m+1)^2-2m=m^2+1\geq 1$ do $m^2\geq 0$ với mọi $m$
Vậy $x_1^2+x_2^2$ min = $1$ khi $m^2=0\Leftrightarrow m=0$
Dạ cho em hỏi tại sao câu x1+x2=-(m+1) mà xuống lại thế là (m+1)^2 ạ

a: Δ=(-2)^2-4(m+2)
=4-4m-8=-4m-4
Để phương trình có nghiệm thì -4m-4>=0
=>4m+4<=0
=>m<=-1
b: x1/x2+x2/x1=-10/3
=>\(\dfrac{x_1^2+x_2^2}{x_1x_2}=\dfrac{-10}{3}\)
=>\(\dfrac{2^2-2\left(m+2\right)}{2}=\dfrac{-10}{3}\)
=>\(\dfrac{4-2m-4}{2}=\dfrac{-10}{3}\)
=>m=10/3

\(cosAOB=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}\)
=>\(2R^2-AB^2=2\cdot R^2\cdot\dfrac{\sqrt{3}}{2}=R^2\cdot\sqrt{3}\)
=>\(AB^2=R^2\cdot\left(2-\sqrt{3}\right)\)
=>\(AB=R\sqrt{2-\sqrt{3}}=\dfrac{R}{\sqrt{2}}\cdot\left(\sqrt{3}-1\right)\)
\(AC=\sqrt{R^2+R^2}=R\sqrt{2}\)
góc OBA=(180-30)/2=75 độ
góc BOC=90+30=120 độ
góc OCA=45 độ
=>góc BAC=360-120-75-45=240-120=120 độ
\(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
=>\(\dfrac{\dfrac{R^2}{2}\cdot\left(4-2\sqrt{3}\right)+2R^2-BC^2}{2\cdot\dfrac{R}{\sqrt{2}}\cdot\left(\sqrt{3}-1\right)\cdot R\sqrt{2}}=\dfrac{-1}{2}\)
=>\(R^2\left(2-\sqrt{3}\right)+2R^2-BC^2=-\dfrac{R}{\sqrt{2}}\cdot\left(\sqrt{3}-1\right)\cdot R\sqrt{2}\)
\(\Leftrightarrow R^2\left(4-\sqrt{3}\right)-BC^2=-2R^2\left(\sqrt{3}-1\right)\)
\(\Leftrightarrow R^2\left(4-\sqrt{3}+2\sqrt{3}-2\right)-BC^2=0\)
=>\(BC^2=R^2\cdot\left(2+\sqrt{3}\right)\)
=>\(BC=R\sqrt{2+\sqrt{3}}\)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC=\dfrac{1}{2}\cdot sin120\cdot\dfrac{R}{\sqrt{2}}\left(\sqrt{3}-1\right)\cdot R\sqrt{2}\)
\(=\dfrac{1}{2}\cdot R^2\cdot\dfrac{\sqrt{3}}{2}\cdot\left(\sqrt{3}-1\right)=R^2\cdot\dfrac{3-\sqrt{3}}{4}\)

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
=>ΔAMB vuông tại M
=>AM vuông góc MB
=>AM vuông góc DC tại K
M là điểm chính giữa của cung AC
nên MA=MC
mà OA=OC
nen OM là trung trực của AC
=>OM vuông góc AC
Xét tứ giác CHMK có
góc CHM+góc CKM=180 độ
=>CHMK là tứ giác nội tiếp
b: Xét tứ giác DMBC có
DC//BM
DM//CB
=>DMBC là hình bình hành
=>DC=MB; DM=BC

Ptr hoành độ của `y=5x-m-4` và `y=x^2` là:
`5x-m-4=x^2`
`<=>x^2-5x+m+4=0` `(1)`
Để `d` và `(P)` cắt nhau tại `2` điểm phân có hoành độ `x_1;x_2`
`<=>` Ptr `(1)` có `2` nghiệm pb
`=>\Delta > 0`
`<=>(-5)^2-4(m+4) > 0`
`<=>m < 9/4`
`=>` Áp dụng Viét có: `{(x_1+x_2=[-b]/a=5),(x_1 .x_2=c/a=m+4):}`
Có: `[x_1]/[x_2]+[x_2]/[x_1]=5`
`<=>[x_1 ^2+x_2 ^2]/[x_1 x _2]=5`
`<=>[(x_1+x_2)^2-2x_1 x_2]/[x_1 x_2]=5`
`<=>[5^2-2(m+4)]/[m+4]=5`
`<=>25-2m-8=5m+20`
`<=>m=-3/7` (t/m)
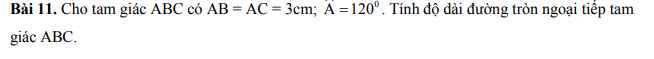
 Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ


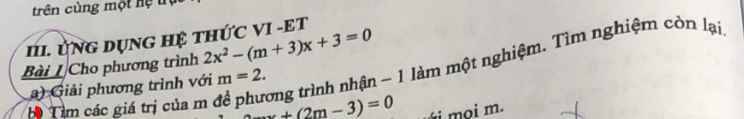





Gọi O là tâm đường tròn ngoại tiếp \(\Delta ABC\)
Vì \(\Delta ABC\) cân tại A nên \(AO\) vừa là đường cao vừa là đường phân giác của \(\widehat{BAC}\)
Suy ra: \(\widehat{CAO}=\dfrac{120}{2}=60^o\) Xét \(\Delta CAO\) có:
\(OA=OC;\widehat{CAO}=60^o\Rightarrow\) \(\Delta CAO\) là tam giác đều
nên \(OA=OC=AC=3cm\)
Nên bán kính đường tròn ngoại tiếp \(\Delta ABC\)
Là \(R=3cm\) Chu vi đường tròn \(\left(O\right)\)
Là \(C=2\pi R=6\pi\left(cm\right)\)