K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
C1
4
2 tháng 2
Câu 6:
Tọa độ A là:
\(\left\{{}\begin{matrix}x+5y-7=0\\x+3y-3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+5y=7\\x+3y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+5y-x-3y=7-3\\x+3y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2\\x=3-3\cdot2=-3\end{matrix}\right.\)
Vậy: A(-3;2)
M(-1;0) là trung điểm của AB
=>\(\left\{{}\begin{matrix}x_A+x_B=2\cdot x_M\\y_A+y_B=2\cdot y_M\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_B-3=2\cdot\left(-1\right)=-2\\y_B+2=0\end{matrix}\right.\Leftrightarrow B\left(1;-2\right)\)
Phương trình đường cao kẻ từ A xuống BC là x+3y-3=0
=>VTPT là (1;3)
=>BC nhận vecto (-3;1) làm vecto pháp tuyến
Phương trình đường thẳng CB là:
-3(x-1)+1(y+2)=0
=>-3x+3+y+2=0
=>-3x+y+5=0
Gọi N là trung điểm của BC
=>N là giao điểm của hai đường thẳng -3x+y+5=0 và x+5y-7=0
Tọa độ N là:
\(\left\{{}\begin{matrix}-3x+y+5=0\\x+5y-7=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-3x+y=-5\\x+5y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3x+y=-5\\3x+15y=21\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-3x+y+3x+15y=-5+21\\x+5y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}16y=16\\x=7-5y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=7-5=2\end{matrix}\right.\)
vậy: N(2;1)
Xét ΔABC có
N,M lần lượt là trung điểm của BC,BA
=>NM là đường trung bình
=>NM//AC
N(2;1); M(-1;0)
=>\(\overrightarrow{NM}=\left(-3;-1\right)=\left(3;1\right)\)
=>AC nhận vecto (3;1) làm vecto chỉ phương
=>VTPT là (-1;3)
Phương trình đường thẳng AC là:
-1(x+3)+3(y-2)=0
=>-x-3+3y-6=0
=>-x+3y-9=0
C1
1
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1 2022
Pt bậc 2 có 2 nghiệm trái dấu khi \(ac< 0\)
\(\Leftrightarrow\left(m^2-4\right)m< 0\)
\(\Leftrightarrow m\in\left(-\infty;-2\right)\cup\left(0;2\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 3 2022
ĐKXĐ: \(x\ge4\)
\(\sqrt{x+11}\ge\sqrt{x-4}+\sqrt{2x-1}\)
\(\Leftrightarrow x+11\ge3x-5+2\sqrt{\left(x-4\right)\left(2x-1\right)}\)
\(\Leftrightarrow8-x\ge\sqrt{2x^2-9x+4}\)
\(\Leftrightarrow\left\{{}\begin{matrix}8-x\ge0\\\left(8-x\right)^2\ge2x^2-9x+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le8\\x^2+7x-60\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le8\\-12\le x\le5\end{matrix}\right.\) \(\Rightarrow-12\le x\le5\)
Kết hợp ĐKXD ta được nghiệm của BPT là: \(4\le x\le5\)
DT
1
29 tháng 12 2021
Câu 5:
\(\Leftrightarrow-x^2+7x-9+2x-9=0\)
\(\Leftrightarrow x^2-9x+18=0\)
=>x=3
=>Chọn A
29 tháng 12 2021
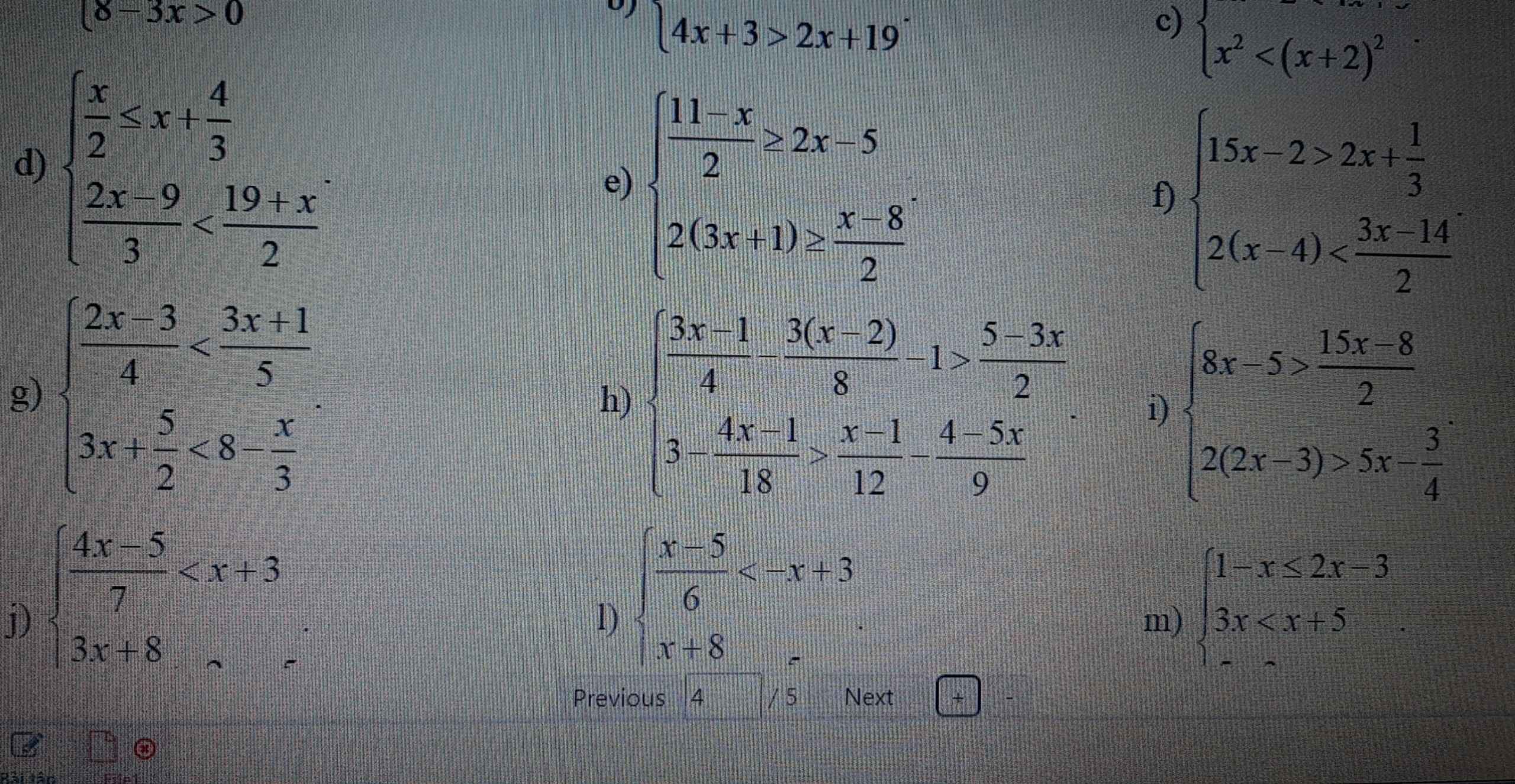
m: \(\Leftrightarrow\left\{{}\begin{matrix}-3x< =-4\\2x< 5\end{matrix}\right.\Leftrightarrow\dfrac{4}{3}< x< \dfrac{5}{2}\)
DT
2
\(x^2-6x+1>\left(2x-3\right)\sqrt{x^2+1}\)
\(\Leftrightarrow\left(x^2+1-9\right)-3\left(2x-3\right)-\left(2x-3\right)\sqrt{x^2+1}>0\)
\(\Leftrightarrow\left(\sqrt{x^2+1}-3\right)\left(\sqrt{x^2+1}+3\right)-\left(2x-3\right)\left(\sqrt{x^2+1}+3\right)>0\)
\(\Leftrightarrow\left(\sqrt{x^2+1}+3\right)\left(\sqrt{x^2+1}-3-\left(2x-3\right)\right)>0\)
\(\Leftrightarrow\sqrt{x^2+1}-2x>0\) (do \(\sqrt{x^2+1}+3>0\) với mọi x)
\(\Leftrightarrow\sqrt{x^2+1}>2x\)
\(\Leftrightarrow\left[{}\begin{matrix}x\le0\\\left\{{}\begin{matrix}x>0\\x^2+1>4x^2\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\le0\\\left\{{}\begin{matrix}x>0\\-\dfrac{\sqrt{3}}{3}< x< \dfrac{\sqrt{3}}{3}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow x< \dfrac{\sqrt{3}}{3}\)
Con ko hiểu ngay chỗ khoanh tròn đỏ ạ. Sao thầy ghi là x<=0 , x>0 mà công thức là x<0, x>=0