
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đường thẳng có dạng: \(y=kx-1\)
Phương trình hoành độ giao điểm: \(x^2+kx-1=0\)
Theo Viet: \(\left\{{}\begin{matrix}x_A+x_B=-k\\x_Ax_B=-1\end{matrix}\right.\) \(\Rightarrow x_A^2+x_B^2=k^2+2\)
\(A\left(x_A;kx_A-1\right);B\left(y_B;kx_B-1\right)\)
Ta có: \(OA^2+OB^2=x_A^2+\left(kx_A-1\right)^2+x_B^2+\left(kx_B-1\right)^2\)
\(=\left(x_A^2+x_B^2\right)\left(k^2+1\right)-2k\left(x_A+x_B\right)+2\)
\(=\left(k^2+2\right)\left(k^2+1\right)-2k.\left(-k\right)+2\)
\(=k^4+5k^2+4\) (1)
\(AB^2=\left(x_A-x_B\right)^2+\left(kx_A-kx_B\right)^2\)
\(=\left(k^2+1\right)\left[\left(x_A+x_B\right)^2-4x_Ax_B\right]\)
\(=\left(k^2+1\right)\left(k^2+4\right)=k^4+5k^2+4\) (2)
(1);(2) \(\Rightarrow OA^2+OB^2=AB^2\) hay tam giác OAB luôn vuông tại O

\(a,\left(d\right)\text{//}\left(d'\right)\Leftrightarrow\left\{{}\begin{matrix}m+1=-m+8\\2m\ne-6\end{matrix}\right.\Leftrightarrow m=\dfrac{7}{2}\\ b,\Leftrightarrow\left\{{}\begin{matrix}m+2\ne-m+8\\2m=-6\end{matrix}\right.\Leftrightarrow m=-3\\ c,\text{Gọi điểm cố định mà }\left(d'\right)\text{ đi qua với mọi }m\ne8\text{ là }A\left(x_0;y_0\right)\\ \Leftrightarrow y_0=\left(8-m\right)x_0+2m\\ \Leftrightarrow mx_0-8x_0-2m+y_0=0\\ \Leftrightarrow m\left(x_0-2\right)+\left(y_0-8x_0\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0-2=0\\y_0-8x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=2\\y_0=16\end{matrix}\right.\\ \Leftrightarrow A\left(2;16\right)\\ \text{Vậy đt đi qua }A\left(2;16\right),\forall m\ne8\)

d. OF//BD nên \(\widehat{FOD}=\widehat{ODB}\)
Mà \(\widehat{ODB}=\widehat{ODF}\Rightarrow\widehat{FOD}=\widehat{ODF}\)
Do đó FOD cân tại F
\(\Rightarrow OF=FD\)
Áp dụng Talet: \(\dfrac{BD}{FD}=\dfrac{BD}{OF}=\dfrac{DH}{HF}\)
\(\Rightarrow\dfrac{BD}{DF}+\dfrac{DF}{HF}=\dfrac{DH}{HF}+\dfrac{DF}{HF}=\dfrac{DH+DF}{HF}=\dfrac{HF}{HF}=1\left(đpcm\right)\)
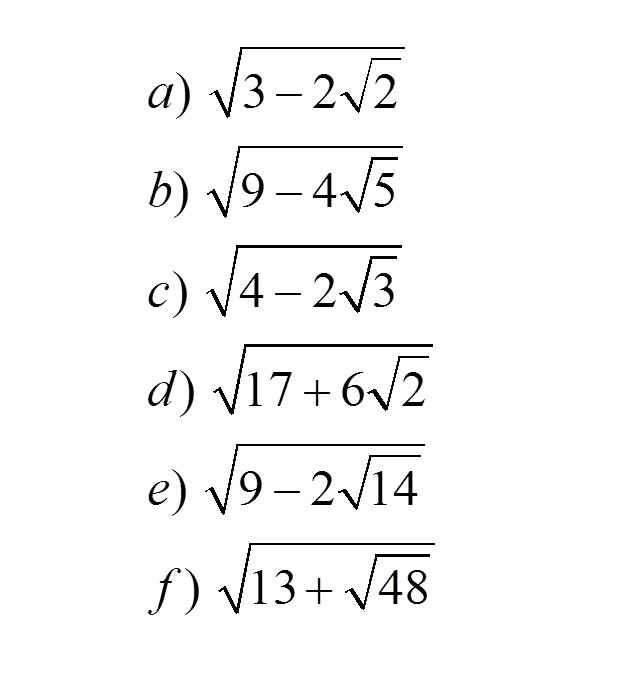



b) \(\sqrt{9-4\sqrt{5}}=\sqrt{9-2\sqrt{20}}=\sqrt{5-2\sqrt{4}.\sqrt{5}+\sqrt{4}}=\sqrt{5}-\sqrt{4}\)
e: \(\sqrt{9-2\sqrt{14}}=\sqrt{7}-\sqrt{2}\)
f: \(\sqrt{13+\sqrt{48}}=2\sqrt{3}+1\)