K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
T
1
2 tháng 1 2022
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM⊥AB
5 tháng 1 2022
Bài 3:
\(a,\) Gọi \(\left(d\right):y=ax+b\) là đt cần tìm
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\\0a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\Leftrightarrow\left(d\right):y=2x+1\)
\(b,\) PT hoành độ giao điểm:
\(-x^2=2x+1\Leftrightarrow\left(x+1\right)^2=0\Leftrightarrow x=-1\Leftrightarrow y=-1\Leftrightarrow A\left(-1;-1\right)\)
Vậy \(A\left(-1;-1\right)\) là tọa độ giao điểm (P) và (d)
Bài 4:
PT có 2 nghiệm \(\Leftrightarrow\Delta'=16-3m\ge0\Leftrightarrow m\le\dfrac{16}{3}\)
Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{8}{3}\\x_1x_2=\dfrac{m}{3}\end{matrix}\right.\)
Mà \(x_1^2+x_2^2=\dfrac{82}{9}\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=\dfrac{82}{9}\)
\(\Leftrightarrow\dfrac{64}{9}-\dfrac{2m}{3}=\dfrac{82}{9}\\ \Leftrightarrow\dfrac{2m}{3}=-2\Leftrightarrow m=-3\left(tm\right)\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
23 tháng 5 2022
a/
Ta có
\(AB\perp OA\)
\(AD\perp OD\) (Trong đường tròn đường thẳng đi qua tâm và đi qua trung điểm của dây cung thì vuông góc với dây cung)
=> B và D cùng nhìn AO dưới 1 góc vuông => B và D cùng nằm trên đường tròn đường kính AO tâm I là trung điểm của AO
=> ABOM là tứ giác nội tiếp
b/ Xét \(\Delta ABC\) và \(\Delta ABD\) có
\(\widehat{BAD}\) chung (1)
\(sđ\widehat{ABC}=\dfrac{1}{2}sđ\) cung AC (góc giữa tiếp tuyến và dây cung)
\(sđ\widehat{ADB}=\dfrac{1}{2}sđ\) cung AC (góc nội tiếp đường tròn)
\(\Rightarrow\widehat{ABC}=\widehat{ADB}\) (2)
Từ (1) và (2) => tg ABC đồng dạng với tg ABD
\(\Rightarrow\dfrac{AB}{AD}=\dfrac{AC}{AB}\Rightarrow AB^2=AC.AD\left(đpcm\right)\)
c/ Xét (I) có
\(\widehat{AEO}=90^o\Rightarrow AE\perp OE\)
Mà E là giao của (I) với (O) => \(E\in\left(O\right)\) => OE là bán kính của (O)
=> AE là tiếp tuyến của đường tròn (O)
d/
Xét tg vuông AOB và tg vuông AOE có
AB=AE (Hai tiếp tuyến cùng xp từ 1điểm)
OB=OE=R
=> tg AOB = tg AOE (Hai tg vuông có 2 cạnh góc vuông bằng nhau) \(\Rightarrow\widehat{AOB}=\widehat{AOE}\)
Xét tg vuông AOB có
\(\cos\widehat{AOB}=\dfrac{OB}{OA}=\dfrac{R}{2R}=\dfrac{1}{2}\Rightarrow\widehat{AOB}=60^0\)
\(\Rightarrow\widehat{BOE}=\widehat{AOB}+\widehat{AOE}=120^o\)
\(\Rightarrow S_{OBE}=\dfrac{\pi R^2.\widehat{BOE}}{360^o}=\dfrac{\pi R^2}{3}\)
27 tháng 9 2021
\(a,ĐK:x\ge0;x\ne9\\ P=\dfrac{\left(3\sqrt{x}+2\right)\left(\sqrt{x}-3\right)+\left(2\sqrt{x}-3\right)\left(\sqrt{x}+1\right)-9\sqrt{x}+15}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}\\ P=\dfrac{3x-7\sqrt{x}-6+2x-\sqrt{x}-3-9\sqrt{x}+15}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}\\ P=\dfrac{5x-17\sqrt{x}+6}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-3\right)\left(5\sqrt{x}-2\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}=\dfrac{5\sqrt{x}-2}{\sqrt{x}+1}\)
\(b,x=4+2\sqrt{3}\Leftrightarrow\sqrt{x}=\sqrt{\left(\sqrt{3}+1\right)^2}=\sqrt{3}+1\\ \Leftrightarrow P=\dfrac{5\sqrt{3}+5-2}{\sqrt{3}+1+1}=\dfrac{5\sqrt{3}+3}{2+\sqrt{3}}=\dfrac{\left(5\sqrt{3}+3\right)\left(2-\sqrt{3}\right)}{4-3}\\ P=7\sqrt{3}-9\)
27 tháng 9 2021
\(c,\sqrt{x}\ge0\Leftrightarrow P=\dfrac{5\sqrt{x}-2}{\sqrt{x}+1}\ge\dfrac{5\cdot0-2}{0+1}=-2\\ P_{min}=-2\Leftrightarrow x=0\)
11 tháng 8 2021
a) \(\dfrac{\sqrt{15}+\sqrt{21}}{\sqrt{5}+\sqrt{7}}=\dfrac{\sqrt{3}.\sqrt{5}+\sqrt{3}.\sqrt{7}}{\sqrt{5}.\sqrt{7}}=\dfrac{\sqrt{3}\left(\sqrt{5}.\sqrt{7}\right)}{\sqrt{5}.\sqrt{7}}=\sqrt{3}\)
11 tháng 8 2021
a) \(\dfrac{\sqrt{15}+\sqrt{21}}{\sqrt{5}+\sqrt{7}}=\dfrac{\sqrt{3}\left(\sqrt{5}+\sqrt{7}\right)}{\sqrt{5}+\sqrt{7}}=\sqrt{3}\)
5 tháng 9 2021
a: Xét tứ giác AMHK có
\(\widehat{MAK}=\widehat{AKH}=\widehat{AMH}=90^0\)
Do đó: AMHK là hình chữ nhật
Suy ra: AH=KM(1)
Xét ΔAHC vuông tại H có
\(AM\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AC=MK^2\)
16 tháng 8 2021
a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKC vuông tại K có KF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AK^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AK là đường cao ứng với cạnh huyền BC, ta được:
\(KB\cdot KC=AK^2\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(AF\cdot AC=KB\cdot KC\)
b: Xét tứ giác AFKE có
\(\widehat{AFK}=\widehat{AEK}=\widehat{EAF}=90^0\)
Do đó: AFKE là hình chữ nhật
Suy ra: \(AK=FE\left(3\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKB vuông tại K có KE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AK^2\left(4\right)\)
Từ \(\left(3\right),\left(4\right)\) suy ra \(AE\cdot AB=FE^2\)
c: Ta có: \(AF\cdot AC+AE\cdot AB+KB\cdot KC\)
\(=AK^2+AK^2+AK^2\)
\(=3\cdot AK^2=3\cdot FE^2\)
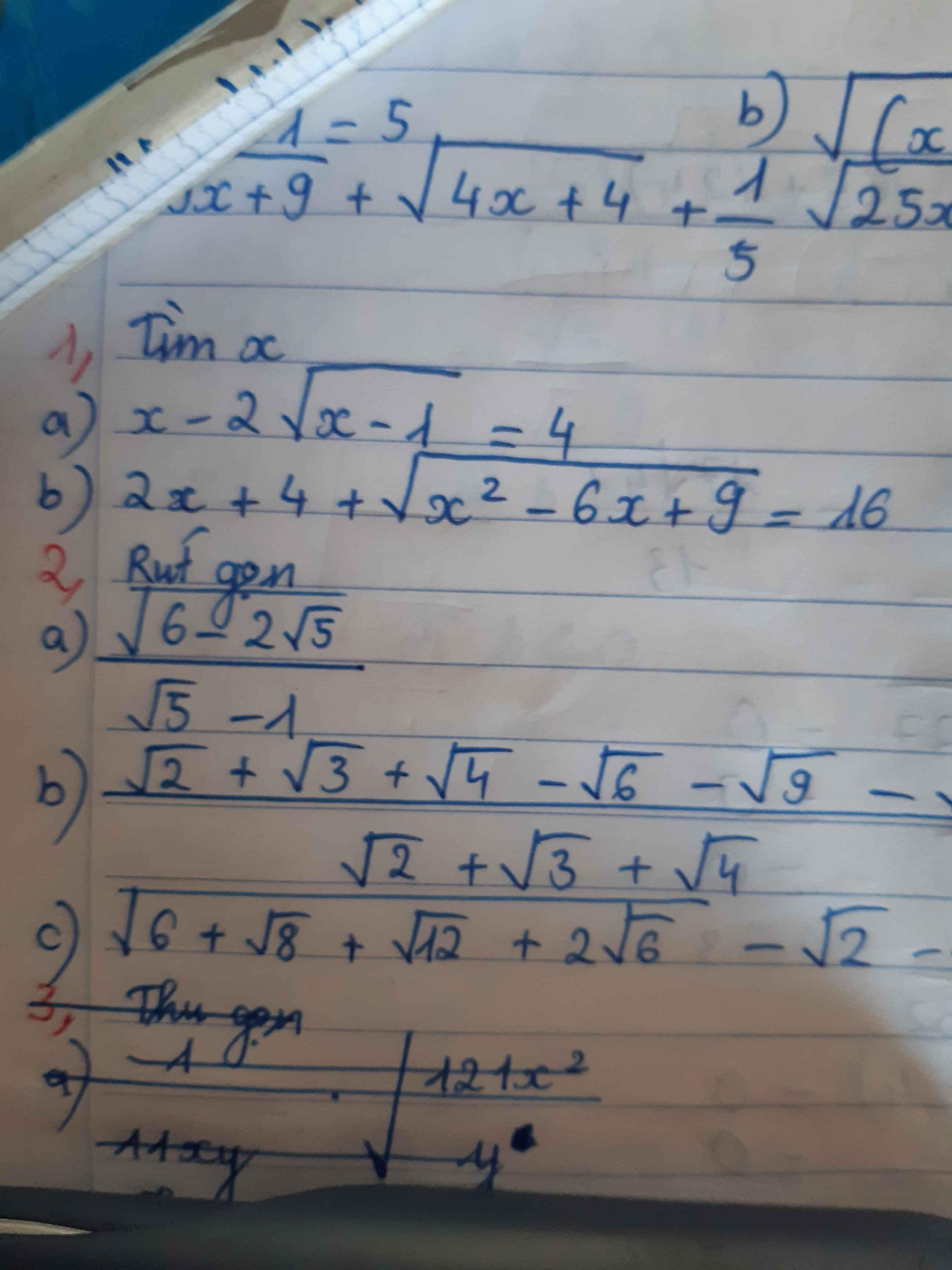
3:
1: Δ=5^2-4(3m-1)
=25-12m+4=-12m+29
Để (1) có hai nghiệm thì -12m+29>=0
=>m<=29/12
2:
(x1-x2)^2=(x1+x2)^2-4x1x2
=(-5)^2-4(3m-1)=25-12m+4=29-12m
x1^3-x2^3+3x1x2=75
=>(x1-x2)^3+3x1x2(x1-x2)+3x1x2=75
=>(x1-x2)[(x1+x2)^2-4x1x2+3x1x2]+3x1x2=75
=>(x1-x2)[(-5)^2-(3m-1)]+3(3m-1)=75
=>(x1-x2)[25-3m+1]+9m-3=75
=>(x1-x2)(26-3m)+9m-78=0
=>(3m-26)(-x1+x2+3)=0
=>m=26/3 hoặc -(x1-x2)=-3
=>m=26/3 hoặc x1-x2=3
=>m=26/3 hoặc (x1+x2)^2-4x1x2=9
=>m=26/3 hoặc (-5)^2-4(3m-1)=9
=>m=26/3 hoặc 25-12m+4=9
=>m=26/3 hoặc 12m=29-9=20
=>m=26/3(loại) hoặc m=5/3(loại)