Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 9:
Gọi số học sinh là $a$. Vì xếp 40 người hay 45 người 1 xe đều không dư nên số học sinh chia hết cho 40 và 45
Do đó số học sinh là bội chung của $40; 45$, hay số học sinh chia hết cho $BCNN(40,45)$
$\Rightarrow a\vdots 360$
$\Rightarrow a=360,720, 1080,....$
Mà $700\leq a\leq 800$ nên $a=720$
Vậy số học sinh là $720$ hs

Câu 13:
a: Trên đoạn thẳng CD, ta có: CM<CD
nên điểm M nằm giữa hai điểm C và D
b: Ta có: điểm M nằm giữa hai điểm C và D
nên CM+MD=CD
hay MD=8-4=4cm
Ta có: điểm M nằm giữa hai điểm C và D
mà MC=MD
nên M là trung điểm của CD
Câu 11:
Vì a chia cho 2;3;4;5 đều dư 1 nên \(a-1\in BC\left(2;3;4;5\right)\)
\(\Leftrightarrow a-1\in\left\{0;60;120;180;...\right\}\)
\(\Leftrightarrow a\in\left\{1;61;121;181;...\right\}\)
mà \(100\le a\le180\)
nên a=121

\(M=\left(-a+b\right)-\left(b+c-a\right)+\left(c-a\right)\)
\(M=-a+b-b-c+a+c-a\)
\(M=\left(-a+a\right)+\left(-b+b\right)+\left(-c+c\right)-a\)
\(M=-a\)
Vì \(a< 0\Rightarrow-a=-\left(-a\right)>0\)
\(\Rightarrow M>0\)


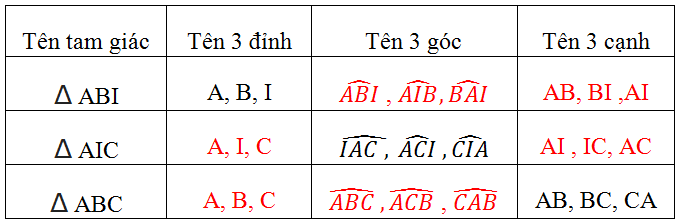
Giải:
|
Tên tam giác |
Tên 3 đỉnh |
Tên 3 góc |
Tên 3 cạnh |
|
|
A,B,I |
|
AB, BI, IA |
|
|
A,I,C |
|
AI, IC, CA |
|
|
A,B,C |
|
AB, BC, CA |

Tập hợp (toán học) Trong toán học, tập hợp có thể hiểu tổng quát là một sự tụ tập của một số hữu hạn hay vô hạn của các đối tượng nào đó




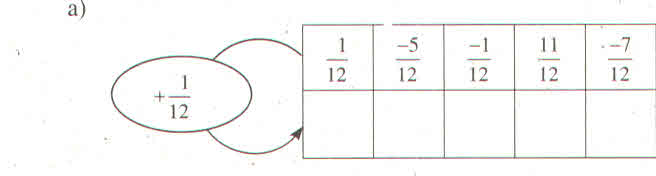
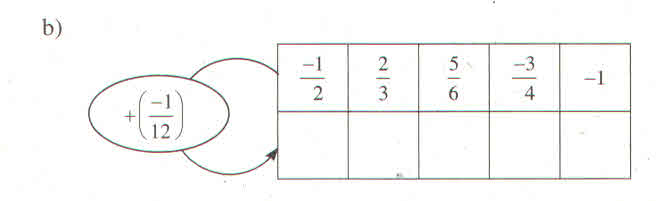


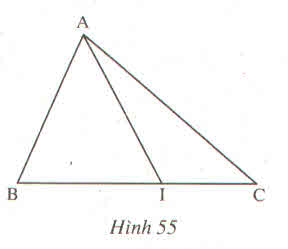

12 tổ nhé !!!!!
Viết thế ai hiểu bạn :)))