
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{a^3}{b\left(c+2\right)}+\dfrac{b}{3}+\dfrac{c+2}{9}\ge3\sqrt[3]{\dfrac{a^3b\left(b+2\right)}{27b\left(c+2\right)}}=a\)
Tương tự: \(\dfrac{b^3}{c\left(a+2\right)}+\dfrac{c}{3}+\dfrac{a+2}{9}\ge b\)
\(\dfrac{c^3}{a\left(b+2\right)}+\dfrac{a}{3}+\dfrac{b+2}{9}\ge c\)
Cộng vế:
\(VT+\dfrac{4\left(a+b+c\right)}{9}+\dfrac{2}{3}\ge a+b+c\)
\(\Rightarrow VT\ge\dfrac{5\left(a+b+c\right)}{9}-\dfrac{2}{3}\ge\dfrac{15}{9}-\dfrac{2}{3}=1\)

a: góc AMB=1/2*180=90 độ
góc AMN+góc AKN=180 độ
=>AMNK là tứ giác nội tiếp
b: ΔCAB vuông tại A có AM vuông góc CB
nên CA^2=MC*CB

b: Xét ΔABH vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HD là đường cao
nên \(AD\cdot AC=AH^2\left(2\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot HC=AH^2\left(3\right)\)
Từ (1), (2) và (3) suy ra \(AE\cdot AB=AD\cdot AC=BH\cdot HC\)

a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM⊥AB


a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKC vuông tại K có KF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AK^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AK là đường cao ứng với cạnh huyền BC, ta được:
\(KB\cdot KC=AK^2\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(AF\cdot AC=KB\cdot KC\)
b: Xét tứ giác AFKE có
\(\widehat{AFK}=\widehat{AEK}=\widehat{EAF}=90^0\)
Do đó: AFKE là hình chữ nhật
Suy ra: \(AK=FE\left(3\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKB vuông tại K có KE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AK^2\left(4\right)\)
Từ \(\left(3\right),\left(4\right)\) suy ra \(AE\cdot AB=FE^2\)
c: Ta có: \(AF\cdot AC+AE\cdot AB+KB\cdot KC\)
\(=AK^2+AK^2+AK^2\)
\(=3\cdot AK^2=3\cdot FE^2\)

b: B>0
=>\(\dfrac{1}{-x+\sqrt{x}}>0\)
=>\(-x+\sqrt{x}>0\)
=>\(x-\sqrt{x}< 0\)
=>\(\sqrt{x}\left(\sqrt{x}-1\right)< 0\)
=>\(\sqrt{x}-1< 0\)
=>\(\sqrt{x}< 1\)
=>0<=x<1
Kết hợp ĐKXĐ, ta được: 0<x<1



 vẽ hình vs làm câu a) . b) thôi ạ, e cần gấp lắm á
vẽ hình vs làm câu a) . b) thôi ạ, e cần gấp lắm á


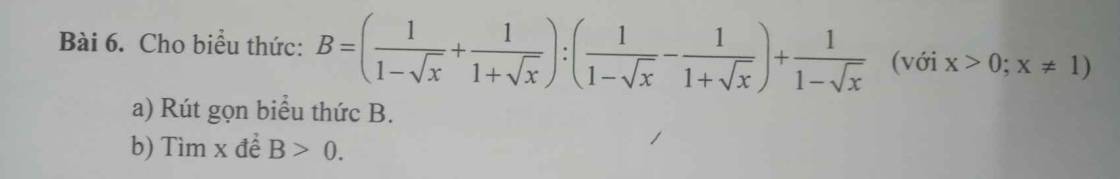 Câu (a) đã rút gọn được là
Câu (a) đã rút gọn được là
a) Xét \(\Delta AEB\) và \(\Delta AFC:\) Ta có: \(\left\{{}\begin{matrix}\angle AEB=\angle AFC=90\\\angle BACchung\end{matrix}\right.\)
\(\Rightarrow\Delta AEB\sim\Delta AFC\left(g-g\right)\)
b) \(\Delta AEB\sim\Delta AFC\Rightarrow\dfrac{AE}{AF}=\dfrac{AB}{AC}\Rightarrow\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét \(\Delta AEF\) và \(\Delta ABC:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{AE}{AB}=\dfrac{AF}{AC}\\\angle BACchung\end{matrix}\right.\)
\(\Rightarrow\Delta AEF\sim\Delta ABC\left(c-g-c\right)\)
c) Xét \(\Delta BFC\) và \(\Delta BDA:\) Ta có: \(\left\{{}\begin{matrix}\angle BFC=\angle BDA=90\\\angle ABCchung\end{matrix}\right.\)
\(\Rightarrow\Delta BFC\sim\Delta BDA\left(g-g\right)\Rightarrow\dfrac{BF}{BD}=\dfrac{BC}{BA}\Rightarrow BF.BA=BC.BD\)
Xét \(\Delta CEB\) và \(\Delta CDA:\) Ta có: \(\left\{{}\begin{matrix}\angle BEC=\angle CDA=90\\\angle ACBchung\end{matrix}\right.\)
\(\Rightarrow\Delta CEB\sim\Delta CDA\left(g-g\right)\Rightarrow\dfrac{CE}{CD}=\dfrac{CB}{CA}\Rightarrow CE.CA=CD.BC\)
\(\Rightarrow BF.BA+CE.CA=BC.BD+BC.CD=BC\left(BD+CD\right)=BC^2\)
????????????