Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

góc MID=90 độ=góc MEN
=>góc IKEN nội tiếp
=>góc MEI=góc MNK
=>ΔMEI đồng dạng vơi ΔMNK
=>EI*MN=NK*ME
Xét ΔMNP có
ME,PI là đường cao
ME cắt PI tại K
=>K là trực tâm
=>NK vuông góc MP tại Q
=>góc NQP=90 độ
góc NIP=góc NQP=90 độ
=>NIQP nội tiếp
=>góc QNP=góc QIP
IKEN nội tiếp
=>gó QNP=góc EIK=góc QIP
=>IK là phân giác của góc EIQ


a, HS tự chứng minh
b, Chứng minh ∆NMC:∆NDA và ∆NME:∆NHA
c, Chứng minh ∆ANB có E là trực tâm => AE ⊥ BN mà có AK ⊥ BN nên có ĐPCM
Chứng minh tứ giác EKBH nội tiếp, từ đó có A K F ^ = A B M ^
d, Lấy P và G lần lượt là trung điểm của AC và OP
Chứng minh I thuộc đường tròn (G, GA)

3, ta có: góc MFA = \(\frac{1}{2}\).(sđ cung AM + sđ cung BQ) (góc có đỉnh nằm trong đường tròn )
và góc MPQ = \(\frac{1}{2}\).sđ cung MQ = \(\frac{1}{2}\).. (sđ cung MB + sđ cung BQ ) (góc nội tiếp)
mà sđ cung AM = sđ cung MB (do M là điểm chính giữa cung AB )
=> góc MFA = góc MPQ
=> góc ngoài MFA tại hai đỉnh có hai góc đối nhau bằng nhau thì tứ giác EFQP là tứ giác nội tiếp hay E,F,P,Q cùng thuộc 1 đường tròn (đpcm)
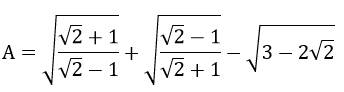
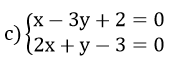
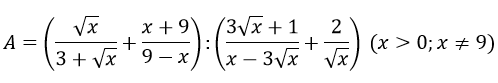
mình mới lớp 6 nên kc bt xin lỗi à
Bài 2:
a) Với m ≠ 0, phương trình trên là phương trình bậc hai ẩn x
Δ' = (m + 1)2 - m(m - 4) = m2 + 2m + 1 - m2 + 4m = 6m + 1
Phương trình có 2 nghiệm x1; x2 khi và chỉ khi Δ' = 6m + 1 ≥ 0
Khi đó, theo định lí Vi-et ta có:
Theo bài ra:
x1 + 4x2 = 3
<=> (x1 + x2 ) + 3x2 = 3
+ 3x2 = 3
=> 5m2 - 2m - 16 = 9m2 - 36m
<=> 4m2 - 34m + 16 = 0
Đối chiếu với điều kiện thỏa mãn
Vậy m = 8, m = thì x1 + 4x2 = 3
b) Ta có:
2(x1 + x2 ) + x1x2 = = 5
Vậy hệ thức liên hệ giữa x1 và x2 không phụ thuộc vào m là 2(x1 + x2 ) + x1x2 = 5
Bài 3:
Gọi số học sinh lớp 9A là x ( học sinh) (x > 8, x ∈ N)
Khi đó, số cây mỗi học sinh phải trồng là:
(cây học sinh )
Do có 8 bạn học sinh vắng mặt nên số cây mỗi bạn phải trồng là
(cây học sinh )
Theo bài ra, mỗi bạn phải trồng thêm 3 cây nên ta có phương trình
=> 480(x - 8) + 3x(x - 8) = 480x
<=> 3x2 - 24x - 3840 = 0
Vậy số học sinh lớp 9A là 40 học sinh
Bài 4:
a) Xét tứ giác AMHN có:
∠AMH = 90o (MH ⊥ AB)
∠ANH = 90o (NH ⊥ AC)
=> ∠AMH + ∠ANH = 180o
=> Tứ giác AMHN là tứ giác nội tiếp
b) Ta có:
ΔAMH vuông tại M: ∠AHM + ∠MAH = 90o
ΔABH vuông tại H: ∠ABC + ∠MAH = 90o
=> ∠AHM = ∠ABC
Do tứ giác AMHN là tứ giác nội tiếp nên ∠AHM = ∠ANM (2 góc nội tiếp cùng chắn cung AM)
=> ∠ABC = ∠ANM
c) Kẻ đường kính AD của (O), Gọi I là giao điểm của AD và MN
ΔANH vuông tại N: ∠AHN + ∠NAH = 90o
ΔACH vuông tại H: ∠AHN + ∠ACB = 90o
=> ∠NAH = ∠ACB
Ta lại có: ∠ACB = ∠ADB (2 góc nội tiếp cùng chắn cung AB)
=> ∠NAH = ∠ADB
Mặt khác: tứ giác AMHN là tứ giác nội tiếp nên ∠AMN = ∠AHN (2 góc nội tiếp cùng chắn cung AN)
=> ∠AMN = ∠ADB
Xét ΔAMI và ΔABD có:
∠BAD là góc chung
∠AMN = ∠ADB
=> ΔAMI ∼ ΔADB
=> ∠ AIM = ∠ABD
Mà ∠ABD = 90o (góc nội tiếp chắn nửa đường tròn)
=> ∠AIM = 90o
Hay OA ⊥ MN
d) Xét tam giác AIN và tam giác ACD có:
∠DAC là góc chung
∠AIN = ∠ACD = 90o
=> ΔAIN ∼ ΔACD
=><=> AI.AD = AC.AN (1)
Xét ΔAHC vuông tại H có HN là đường cao
=> AC. AN = AH2 (2)
Từ (1) và (2) => AI.AD = AH2 <=> AI.AD = 2R2
<=> AI.2R = 2R2 <=> AI = R <=> I ≡ O
Vậy M, N, O thẳng hàng.
Bài 5:
Do a, b > 0 nên ta có:
Dấu bằng xảy ra khi:
Vậy GTLN của P là 2√2, đạt được khi a = b = 1.