Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Khi phương trình ax2 + bx + c = 0 có a và c trái dấu thì ac < 0, suy ra –ac > 0; hơn nữa b2 ≥ 0. Do đó ∆ = b2 – 4ac > 0. Vậy phương trình có hai nghiệm phân biệt.
Áp dụng:
a) Phương trình 15x2 + 4x – 2005 = 0 có a = 15, c = -2005 trái dấu nhau nên phương trình có hai nghiệm phân biệt.
b) Phương trình x2 - √7x + 1890 = 0 có a =
và c = 1890 trái dấu nhau nên phương trình có hai nghiệm phân biệt.
a) Phương trình 15 x 2 + 4 x – 2005 = 0 có a = 15; c = -2005 trái dấu
⇒ Phương trình có hai nghiệm phân biệt.
b) Phương trình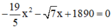 
có 
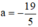; c = 1890 trái dấu
⇒ Phương trình có hai nghiệm phân biệt.
Phương trình 15x2 + 4x – 2005 = 0 có a = 15; c = -2005 trái dấu
⇒ Phương trình có hai nghiệm phân biệt.
a) Ta có
Δ′=12−3(−7)=22>0
Vậy ptrinh luôn có 2 nghiệm phân biệt.
a) Phương trình 4 x 2 + 2 x − 5 = 0
Có a = 4; b = 2; c = -5, a.c < 0
⇒ Phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-et ta có: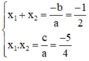 
b) Phương trình . 9 x 2 − 12 x + 4 = 0
Có a = 9; b' = -6; c = 4 ⇒ Δ 2 = ( - 6 ) 2 - 4 . 9 = 0
⇒ Phương trình có nghiệm kép x 1 = x 2 .
Theo hệ thức Vi-et ta có: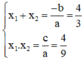 
c) Phương trình 5 x 2 + x + 2 = 0
Có a = 5; b = 1; c = 2 ⇒ Δ = 1 2 − 4.2.5 = − 39 < 0
⇒ Phương trình vô nghiệm.
d) Phương trình 159 x 2 − 2 x − 1 = 0
Có a = 159; b = -2; c = -1; a.c < 0
⇒ Phương trình có hai nghiệm phân biệt x 1 ; x 2 .
Theo hệ thức Vi-et ta có: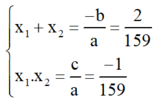 
Phương trình 4x2 + 2x – 5 = 0
Có a = 4; b = 2; c = -5, a.c < 0
⇒ Phương trình có hai nghiệm x1; x2
Theo hệ thức Vi-et ta có: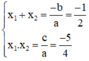 
Đáp án B
Ta có:
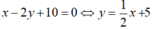
Nên tập nghiệm của phương trình x – 2y + 10 = 0 được biểu diễn bởi đường thẳng (d1):
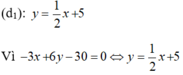
Nên tập nghiệm của phương trình -3x +6y – 30= 0 được biểu diễn bởi đường thẳng (d2):
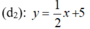
Do đó, nên hệ phương trình đã cho có vô số nghiệm.
Phương trình 5x2 + x + 2 = 0
Có a = 5; b = 1; c = 2 ⇒ Δ = 12 – 4.2.5 = -39 < 0
⇒ Phương trình vô nghiệm.
Phương trình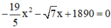
có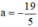 
; c = 1890 trái dấu
⇒ Phương trình có hai nghiệm phân biệt.