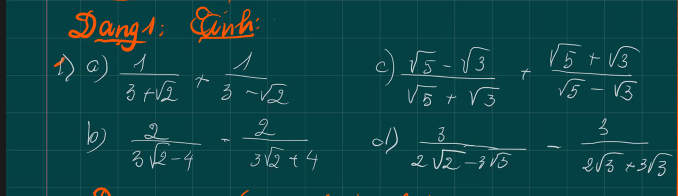K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 1 2022
1. \(\left\{{}\begin{matrix}4x-2y=3.\\6x-3y=5.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}12x-6y=9.\\12x-6y=10.\end{matrix}\right.\)\(\Leftrightarrow x\in\phi.\)
2. \(\left\{{}\begin{matrix}2x+3y=5.\\4x+6y=10.\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}8x+12y=20.\\8x+12y=20.\end{matrix}\right.\)\(\Leftrightarrow x\in\phi.\)
3. \(\left\{{}\begin{matrix}3x-4y+2=0.\\5x+2y=14.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x-4y=-2.\\5x+2y=14.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x-4y=-2.\\10x+4y=28.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x-4y=-2.\\13x=26.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=2.\\x=2.\end{matrix}\right.\)
4. \(\left\{{}\begin{matrix}2x+5y=3.\\3x-2y=14.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x+15y=9.\\6x-4y=28.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x+5y=3.\\19y=-19.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=4.\\y=-1.\end{matrix}\right.\)
7. \(\left\{{}\begin{matrix}\dfrac{x}{y}=\dfrac{2}{3}.\\x+y-10=0.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x-2y=0.\\x+y=10.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2y=0.\\3x+3y=30.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=10.\\-5y=-30.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4.\\y=6.\end{matrix}\right.\)
TT
12 tháng 2 2016
6a1b không chia hết cho 2 nhưng chia hết cho 5 thì có tận cùng là 5.
Ta có số 6a15 vì số này chia hết cho 9 nên 6+a+1+5 phải chia hết cho 9 hay 12+a chia hết cho 9 do đó a=6 .
Ta có số 6615
20 tháng 9 2021
a) \(=\dfrac{3-\sqrt{2}+3+\sqrt{2}}{9-2}=\dfrac{6}{7}\)
b) \(=\dfrac{\left(\sqrt{5}-\sqrt{3}\right)^2+\left(\sqrt{5}+\sqrt{3}\right)^2}{\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)}=\dfrac{5-2\sqrt{15}+3+5+2\sqrt{15}+3}{5-3}=\dfrac{16}{2}=8\)
c) \(=\dfrac{2\left(3\sqrt{2}+4\right)-2\left(3\sqrt{2}-4\right)}{\left(3\sqrt{2}-4\right)\left(3\sqrt{2}+4\right)}=\dfrac{6\sqrt{2}+8-6\sqrt{2}+8}{18-16}=\dfrac{16}{2}=8\)
d) \(=\dfrac{3\left(2\sqrt{2}+3\sqrt{3}\right)-3\left(2\sqrt{2}-3\sqrt{3}\right)}{\left(2\sqrt{2}-3\sqrt{3}\right)\left(2\sqrt{2}+3\sqrt{3}\right)}=\dfrac{6\sqrt{2}+9\sqrt{3}-6\sqrt{2}+9\sqrt{3}}{8-27}=\dfrac{18\sqrt{3}}{-19}=-\dfrac{18\sqrt{3}}{19}\)
20 tháng 9 2021
\(a,=\dfrac{3-\sqrt{2}+3+\sqrt{2}}{\left(3+\sqrt{2}\right)\left(3-\sqrt{2}\right)}=\dfrac{6}{3^2-\left(\sqrt{2}\right)^2}=\dfrac{6}{7}\\ b,=\dfrac{2\left(3\sqrt{2}+4\right)-2\left(3\sqrt{2}-4\right)}{\left(3\sqrt{2}-4\right)\left(3\sqrt{2}+4\right)}=\dfrac{6\sqrt{2}+8-6\sqrt{2}+8}{18-16}=\dfrac{16}{2}=8\\ c,=\dfrac{\left(\sqrt{5}-\sqrt{3}\right)^2+\left(\sqrt{5}+\sqrt{3}\right)^2}{\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)}=\dfrac{8-2\sqrt{15}+8+2\sqrt{15}}{2}=\dfrac{16}{2}=8\)
\(d,=\dfrac{3\left(2\sqrt{2}+3\sqrt{3}\right)}{8-27}-\dfrac{3}{5\sqrt{3}}=\dfrac{6\sqrt{2}+9\sqrt{3}}{-19}-\dfrac{\sqrt{3}}{5}\\ =\dfrac{-30\sqrt{2}-45\sqrt{3}-19\sqrt{3}}{95}=\dfrac{-30\sqrt{2}-64\sqrt{2}}{95}\)
13 tháng 3 2021
Giả sử tồn tại x, y, z, t thỏa mãn.
Ta chứng minh bổ đề: Cho \(a,b\in\mathbb{Z}\). Khi đó \(a^2+b^2\vdots 3\Leftrightarrow a,b\vdots 3\).
Thật vậy, ta thấy nếu \(a,b\vdots 3\Rightarrow a^2+b^2\vdots 3\).
Nếu \(a^2+b^2\vdots 3\): Do \(a^2,b^2\equiv0;1\left(mod3\right)\) nên ta phải có \(a^2,b^2\equiv0\left(mod3\right)\Rightarrow a,b⋮3\).
Bổ đề dc cm.
Trở lại bài toán: Ta có 2019 chia hết cho 3 nên \(x^2+y^2⋮3\Rightarrow x,y⋮3\Rightarrow x^2+y^2⋮9\).
Mà 2019 không chia hết cho 9 nên \(z^2+t^2⋮3\Leftrightarrow z,t⋮3\).
Đặt x = 3x', y = 3y', z = 3z', t = 3t'.
Ta có \(2019=\dfrac{x^2+y^2}{z^2+t^2}=\dfrac{x'^2+y'^2}{z'^2+t'^2}\).
Cmtt, ta có \(x',y',z',t'⋮3\).
Lặp lại nhiều lần như vậy, ta có \(x,y,z,t⋮3^k\forall k\in N\).
Do đó x = y = z = t = 0 (vô lí).
Vậy không tồn tại...