Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
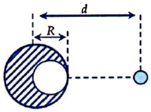
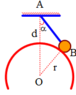
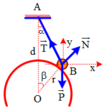
Phần khoét đi, nếu đặt lại chỗ cũ sẽ hút m lực hấp dẫn:
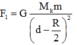
Lực hấp dẫn do cả quả cầu đặc tác dụng lên m:
![]()
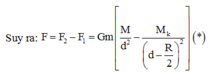
Do quả cầu đồng chất nên:
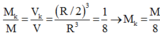
Thay vào (*) rồi biến đổi ta được
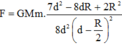

Đáp án A.
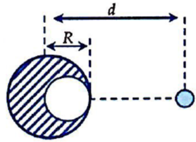
Phần khoát đi, nếu đặt lại chỗ cũ sẽ hút m lực hấp dẫn: F 1 = G M k m ( d - R 2 ) 2
Lực hấp dẫn do cả quả cầu đặc tác dụng lên m: F 2 = G M m d 2
Suy ra:
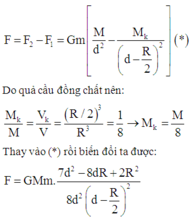

Có hình ko bạn? Đề bài ko có dấu chấm dấu phẩy nên đọc ko hiểu gì :v

![]()
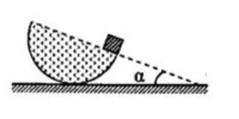
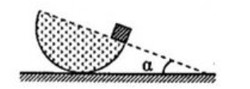
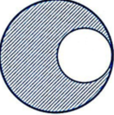
Gọi x là khoảng cách từ tâm hình tròn lớn O đến trọng tâm phần còn lại O1.
Theo quy tắc hợp lực song song:
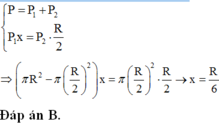

Do tính đối xứng G nằm trên đường thẳng OO’ về phía đầy.
Trọng tâm của đĩa nguyên vẹn là tâm O; trọng tâm của đĩa bị khoét là O’.
P → là hợp lực của hai lực P → 1 , P → 2 .
O G O O ' = P 2 P 1 = m 2 m 1 = V 2 V 1 = S 2 S 1 = π R 2 4 3 π R 2 4 = 1 3 ⇒ O G = R 6

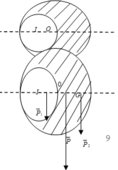
Giả sử ta khoét thêm một lỗ tròn bán kính R/2 nữa đối xứng với lỗ tròn đã khoét lúc đầu (H.III.6G)
Gọi P → là trọng lượng của đĩa bán kính R khi chưa bị khoét, P 1 → là trọng lượng của đĩa nhỏ có bán kính R/2 và P 2 → là trọng lượng của phần đĩa còn lại sau hai lần khoét, ta có:
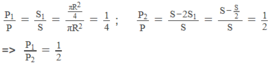
Do tính chất đối xứng, trọng tâm phần đĩa còn lại sau hai lần khoét thì trùng với tâm O của đĩa khi chưa khoét, còn trọng tâm của đĩa nhỏ mà ta giả sử khoét thêm thì ở tâm O 1 của nó. Gọi G là trọng tâm của đĩa sau khi bị khoét một lỗ tròn. Ta có hệ phương trình
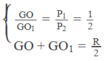
Giải ra ta được: G O 1 = R/3 và GO = R/6
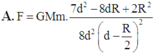
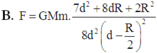
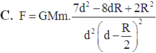


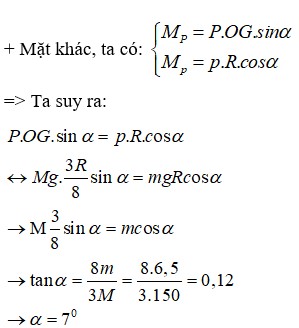

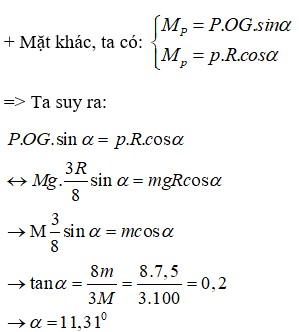
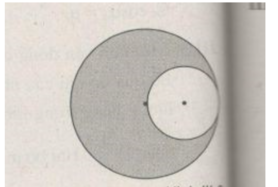
Ý tưởng chung là "bù" phần bị khoét, coi như nó đặc, như vậy ta luôn có \(I_O+I_{O'}=I_C\) với \(I_C\) là mômen quán tính của hình cầu đặc hoàn hảo khi chưa bị khoét \(\Rightarrow I_O=I_C-I_{O'}\)
Ta có khối lượng đã bị khoét:
\(\frac{m'}{m}=\left(\frac{r}{R}\right)^3\Rightarrow m'=\frac{m}{8}\)
TH1: Trục quay qua \(OO':\)
\(I_O=I_C-I_{O'}=\frac{2}{5}mR^2-\frac{2}{5}m'.r=\frac{2}{5}mR^2-\frac{2}{5}.\frac{m}{8}.\left(\frac{R}{2}\right)^2=\frac{31}{80}mR^2\)
TH2: Chứa O và vuông góc OO':
Áp dụng định lý Steiner-Huyghen, momen quán tính của phần tưởng tượng \(O'\) với trục qua O và vuông góc OO':
\(I_{O'}=\frac{2}{5}\frac{m}{8}\left(\frac{R}{2}\right)^2+\frac{m}{8}.\left(\frac{R}{2}\right)^2=\frac{7}{160}mR^2\)
\(\Rightarrow I_O=I_C-I_{O'}=\frac{2}{5}mR^2-\frac{7}{160}mR^2=\frac{57}{160}mR^2\)
- TH3: Chứa O' và vuông góc OO':
Áp dụng định lý Steiner-Huyghen, momen của khối chưa bị khoét \(I_C\) với trục mới:
\(I_C=\frac{2}{5}mR^2+m.\left(\frac{R}{2}\right)^2=\frac{13}{20}mR^2\)
\(\Rightarrow I_O=I_C-I_{O'}=\frac{13}{20}mR^2-\frac{2}{5}.\frac{m}{8}.\left(\frac{R}{2}\right)^2=\frac{51}{80}mR^2\)
...