Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ \(d\left(M;d\right)=\frac{\left|1-1-5\right|}{\sqrt{1^2+1^2}}=\frac{5\sqrt{2}}{2}\)
b/ Trục Ox có pt \(y=0\)
\(\Rightarrow d\left(M;Ox\right)=\frac{\left|0+2\right|}{\sqrt{0^2+1^2}}=2\)
c/ \(2x=3\Leftrightarrow2x-3=0\)
\(d\left(M;d\right)=\frac{\left|-3.2-3\right|}{\sqrt{2^2+0^2}}=\frac{9}{2}\)
d/ \(\left\{{}\begin{matrix}x=-2+2t\\y=5-t\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}t=\frac{x+2}{2}\\t=5-y\end{matrix}\right.\)
\(\Rightarrow\frac{x+2}{2}=5-y\Leftrightarrow x+2y-8=0\)
\(\Rightarrow d\left(M;d\right)=\frac{\left|5+2.\left(-2\right)-8\right|}{\sqrt{1^2+2^2}}=\frac{7\sqrt{5}}{5}\)

\(1/\)
\(M\left(3;5\right);d:x+y+1=0\)
\(\)Gọi khoảng cách từ M đến d là \(l\)
\(l\left(M;d\right)=\dfrac{\left|x_M+y_M+1\right|}{\sqrt{1^2+1^2}}=\dfrac{\left|3+5+1\right|}{\sqrt{1^2+1^2}}=\dfrac{9\sqrt{2}}{2}\)
\(M\left(2;3\right);d:\left\{{}\begin{matrix}x-2t\\y=2+3t\end{matrix}\right.\)
d qua \(M\left(2;3\right)\) có \(VTCP\overrightarrow{u}=\left(-2;3\right)\Rightarrow VTPT\overrightarrow{n}=\left(3;2\right)\)
\(PTTQ\) của \(\Delta:3\left(x-2\right)+2\left(y-3\right)=0\)
\(\Rightarrow3x-6+2y-6=0\)
\(\Rightarrow3x+2y-12=0\)
Gọi khoảng cách từ M đến d là \(l\)
\(l\left(M;d\right)=\dfrac{\left|3.x_M+2.y_M-12\right|}{\sqrt{3^2+2^2}}=\dfrac{\left|3.2+2.3-12\right|}{\sqrt{3^2+2^2}}=0\)

Lời giải:
Vì $A\in (d_1)$ nên gọi tọa độ của $A$ là $(a, 2a-2)$
Vì $B\in (d_2)$ nên gọi tọa độ của $B$ là $(b, -b-3)$
$M$ là trung điểm của $AB$ nên:
\(3=x_M=\frac{x_A+x_B}{2}=\frac{a+b}{2}\Rightarrow a+b=6(1)\)
\(0=y_M=\frac{y_A+y_B}{2}=\frac{2a-2-b-3}{2}\Rightarrow 2a-b=5(2)\)
Từ $(1); (2)\Rightarrow a=\frac{11}{3}; b=\frac{7}{3}$
Khi đó: $A=(\frac{11}{3}, \frac{16}{3})$
Vì $A, M\in (d)$ nên VTCP của (d) là $\overrightarrow{MA}=(\frac{2}{3}, \frac{16}{3})$
$\Rightarrow \overrightarrow{n_d}=(\frac{-16}{3}, \frac{2}{3})$
PTĐT $(d)$ là:
$\frac{-16}{3}(x-3)+\frac{2}{3}(y-0)=0$
$\Leftrightarrow -8x+y+24=0$

9. Cho đg thẳng d 3x +4y -5=0 và 2 điểm A(1;3) , B(2;m). Định m để A và B nằm cùng phía đối với d.
Hai điểm A và B nằm cùng phía với (d)
\(\Leftrightarrow\)(3.1+4.3-5).(3.2+4.m-5)>0
\(10\left(6+4m-5\right)>0\)
\(60+40m-50>0\Rightarrow m>-\frac{1}{4}\)
10. Cho tam giác ABC với A(1;3) , B(-2;4) ,C(-1;5) và đg thẳng d : 2x -3y +6=0. Đg thẳng d cắt cạnh nào của tg ABC?
(bạn xem lại đề)
11. Khoảng cách từ điểm M (1;-1) đến đg thẳng denta 3x -4y -17=0 là:
\(d_{\left(M,\Delta\right)}=\frac{\left|ax_0+by_0+c\right|}{\sqrt{a^2+b^2}}=\frac{\left|3.1-4.\left(-1\right)-17\right|}{\sqrt{3^2+\left(-4\right)^2}}\)\(=2\)
Câu 12,13 tương tự vậy
14. Khoảng cách từ điểm M(0;2) đến đg thẳng denta x =1 +3t ; y = 2+4t là:
\(\Delta:\left\{{}\begin{matrix}x=1+3t\\y=2+4t\end{matrix}\right.\)
PTTQ của delta:\(4x-3y+2=0\)
áp dụng ct:
\(d_{\left(M,\Delta\right)}=\frac{\left|ax_0+by_0+c\right|}{\sqrt{a^2+b^2}}=\frac{4}{5}\)
( bạn xem lại đáp án)
16. Tính diện tích tg ABC biết A(-2;1) , B(1;2) , C (2;-4)
sABC= 5,5

M thuộc d nên tọa độ có dạng:
\(M\left(t+3;t+2\right)\) với \(t>-3\)
Áp dụng công thức khoảng cách:
\(d\left(M;\Delta\right)=\frac{\left|2\left(t+3\right)-\left(t+2\right)-3\right|}{\sqrt{2^2+\left(-1\right)^2}}=2\sqrt{5}\)
\(\Leftrightarrow\left|t+1\right|=10\Rightarrow\left[{}\begin{matrix}t=9\\t=-11\left(l\right)\end{matrix}\right.\)
\(\Rightarrow M\left(12;11\right)\)
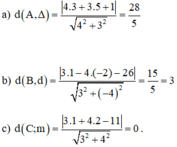

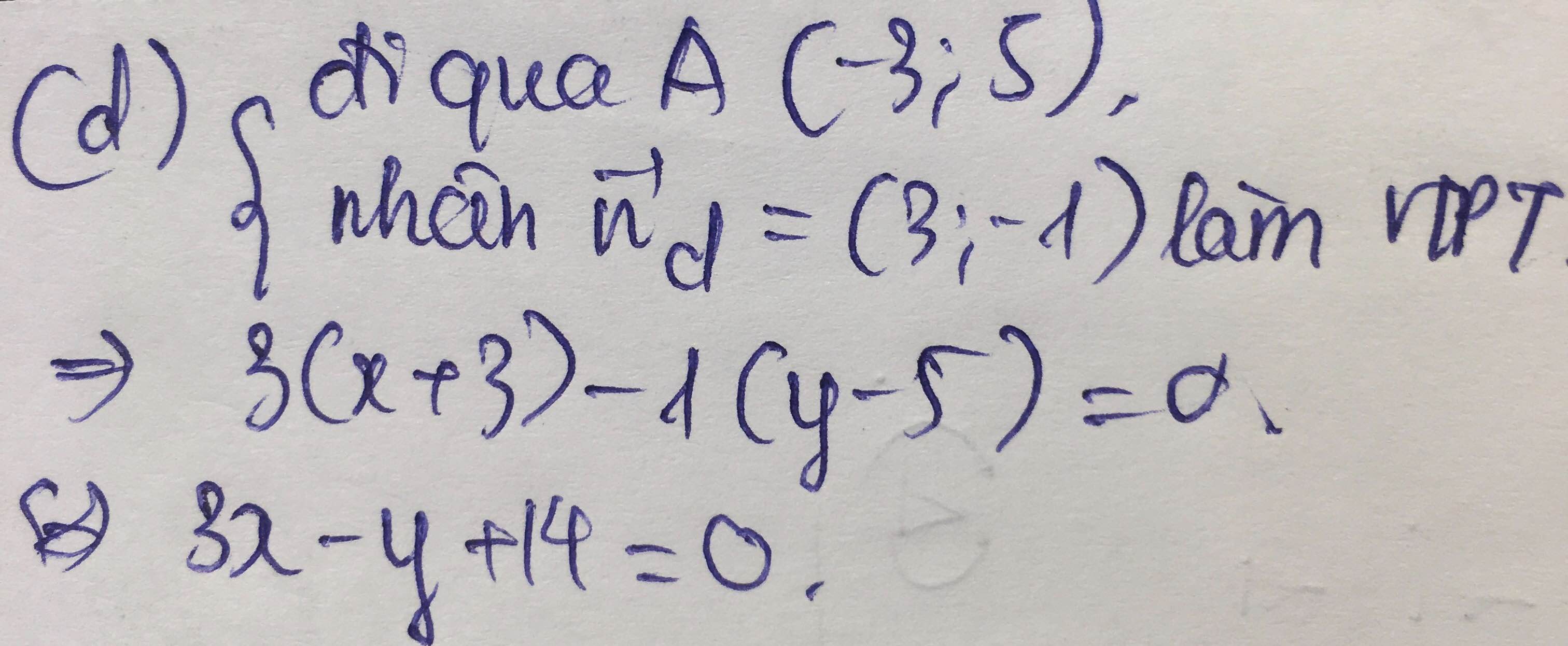
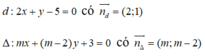
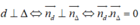
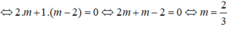
Chọn A.
Khoảng cách từ điểm M(3;0) đường thẳng Δ: 2x + y + 4 = 0 là: