Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
.
Đáp án A
Phương trình hoành độ gioa điểm của d và (C) là
Suy ra 
suy ra 
Dễ dàng tính được 
+ Giả sử M( x 0 ; y 0 ) ∈ C suy ra y 0 = 2 x 0 + 3 x 0 + 1
+Ta có
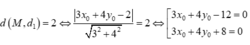
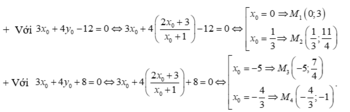
Ta tìm được 4 điểm M suy ra có 4 tiếp tuyến.
Chọn C.
- Giả sử 
- Ta có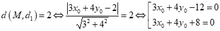 
- Với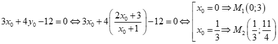 
- Với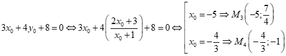 
Suy ra có 4 tiếp tuyến.
Chọn C.
3.
\(y'=3x^2-3\Rightarrow k=y'\left(1\right)=0\)
4.
\(y'=-2x+2=0\Rightarrow x=1\)
\(y''=-2< 0\Rightarrow x=1\) là điểm cực đại
Vậy hàm số ko có điểm cực tiểu
5.
Pt hoành độ giao điểm: \(\frac{x^2-4}{x-1}=0\Rightarrow x^2-4=0\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\) có 2 giao điểm với trục Ox
6.
\(\lim\limits_{x\rightarrow6}\frac{x+4}{-x+6}=\infty\Rightarrow x=6\) là tiệm cận đứng
7.
\(y'=2x+2\)
Tiếp tuyến song song với trục Oy nên có hệ số góc \(k=0\)
\(\Rightarrow2x+2=0\Rightarrow x=-1\Rightarrow y=-4\)
Vậy pttt có dạng \(y+4=0\)
9.
Hai tiệm cận có pt lần lượt \(x=1\) và \(y=1\)
Tích khoảng cách từ điểm M đến 2 tiệm cận:
\(d=\left|x_0-1\right|.\left|\frac{x_0+4}{x_0-1}-1\right|=\left|\left(x_0-1\right).\frac{5}{\left(x_0-1\right)}\right|=5\)
10.
Hàm \(y=2x\) có \(y'=2>0\) đồng biến trên miền xác định
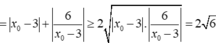
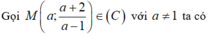
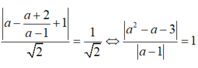
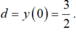
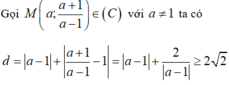
Đáp án D
Khoảng cách từ M đến d là h(M;d) cho bởi