Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Khoảng cách đó gợi nên khái niệm khoảng cách giữa hai mặt phẳng song song.
b)
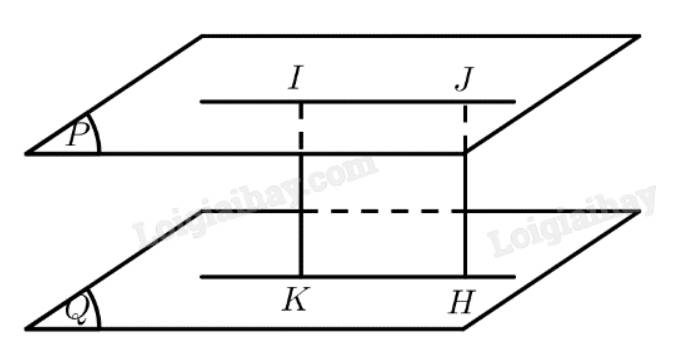
Trên mặt phẳng \(\left( P \right)\) lấy điểm \(J\) khác \(I\).
Kẻ \(JH \bot \left( Q \right)\left( {H \in \left( Q \right)} \right)\)
\( \Rightarrow HKIJ\) là hình chữ nhật \( \Rightarrow IK = JH\)
\( \Rightarrow d\left( {I,\left( Q \right)} \right) = d\left( {J,\left( Q \right)} \right)\)
Vậy khoảng cách \(IK\) từ điểm \(I\) đến mặt phẳng \(\left( Q \right)\) không phụ thuộc vào vị trí của điểm \(I\) trong mặt phẳng \(\left( P \right)\).

a: \(a\perp\left(Q\right)\)
b: Hai mặt phẳng (P) và (Q) có vuông góc với nhau

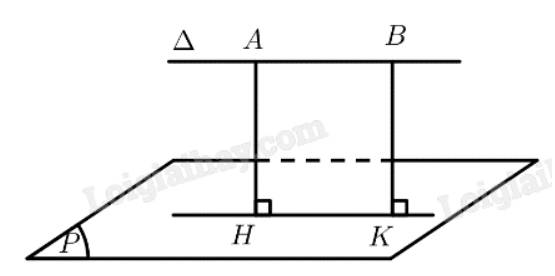
a) Trên đường thẳng \(\Delta \) lấy điểm \(B\) khác \(A\).
Kẻ \(AH \bot \left( P \right),BK \bot \left( P \right)\left( {H,K \in \left( P \right)} \right)\)
\( \Rightarrow ABKH\) là hình chữ nhật \( \Rightarrow AH = BK\)
\( \Rightarrow d\left( {A,\left( P \right)} \right) = d\left( {B,\left( P \right)} \right)\)
Vậy khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( P \right)\) không phụ thuộc vào vị trí của điểm \(A\) trên đường thẳng \(\Delta \).
b) Khoảng cách đó gợi nên khái niệm khoảng cách giữa đường thẳng và mặt phẳng song song.

a: Gọi \(A,B\in a\)
A',B' lần lượt là hình chiếu của A,B trên (P)
\(d\subset\left(P\right)\) nên \(AB\subset\left(P\right)\)
=>d vuông góc A'A
Do đó: nếu d vuông góc a' thì d vuông góc mp(a,a')
=>d vuông góc a
b: Nếu d vuông góc a thì d vuông góc mp(a,a')
=>d vuông góc a'

a) • Ta có: M ∈ b và (P) ∩ (Q) = b;
Suy ra M ∈ (P).
Mà M ∈ (M, a)
Do đó M là giao điểm của (P) và (M, a).
Lại có b’ = (P) ∩ (M, a)
Suy ra đường thẳng b’ đi qua M.
Tương tự ta cũng chứng minh được b’’ đi qua điểm M.
• Ta có: a // (P);
a ⊂ (M, a)
(M, a) ∩ (P) = b’
Do đó a // b’.
Tương tự ta cũng có a // b’’.
Do đó b’ // b’’.
Mặt khác: (P) ∩ (Q) = b;
(M, a) ∩ (P) = b’;
(M, a) ∩ (Q) = b’’;
b // b’’.
Do đó b // b’ // b’’.
Mà cả ba đường thẳng cùng đi qua điểm M nên ba đường thẳng này trùng nhau.
b) Vì a // b’ nên a // b (do b ≡ b’).
tham khảo
Ta có:\(a//\left(P\right)\)
\(a//\left(Q\right)\)
\(\left(P\right)\cap\left(Q\right)=b\)
Do đó theo hệ quả định lí \(2\) ta có \(a//b\).

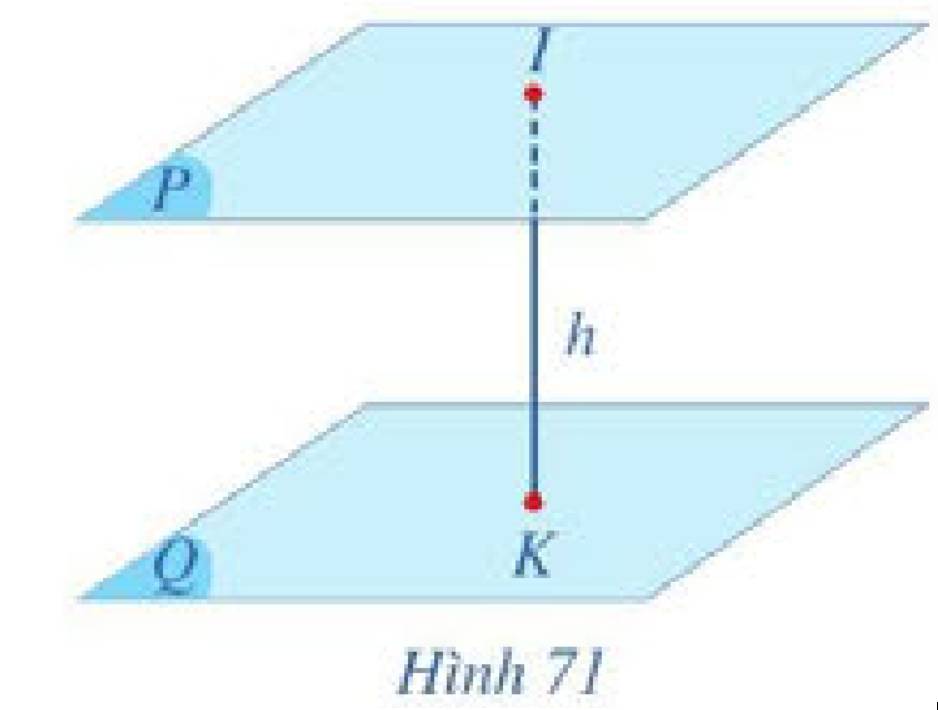

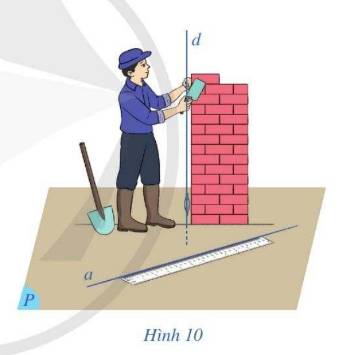
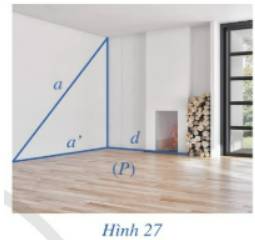


Gợi nên khái niệm khoảng cách từ một điểm đến một mặt phẳng