K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 2 2022
Phương trình hoành độ giao điểm là:
\(x^2-2mx+m^2-m=0\)
a: Để (P) cắt (d) tại hai điểm phân biệt thì \(\left(-2m\right)^2-4\left(m^2-m\right)>0\)
=>4m>0
hay m>0
b: Để (P) cắt (d) tại hai điểm nằm về hai phía của trục tung thì \(m^2-m< 0\)
=>0<m<1
HT
0
29 tháng 10 2021
\(\left\{{}\begin{matrix}x=5-y\\y\left(5-y\right)=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1\\y=4\end{matrix}\right.\\\left\{{}\begin{matrix}x=4\\y=1\end{matrix}\right.\end{matrix}\right.\)
28 tháng 1 2022
a) Thay m = -2 vào (P) ta có:
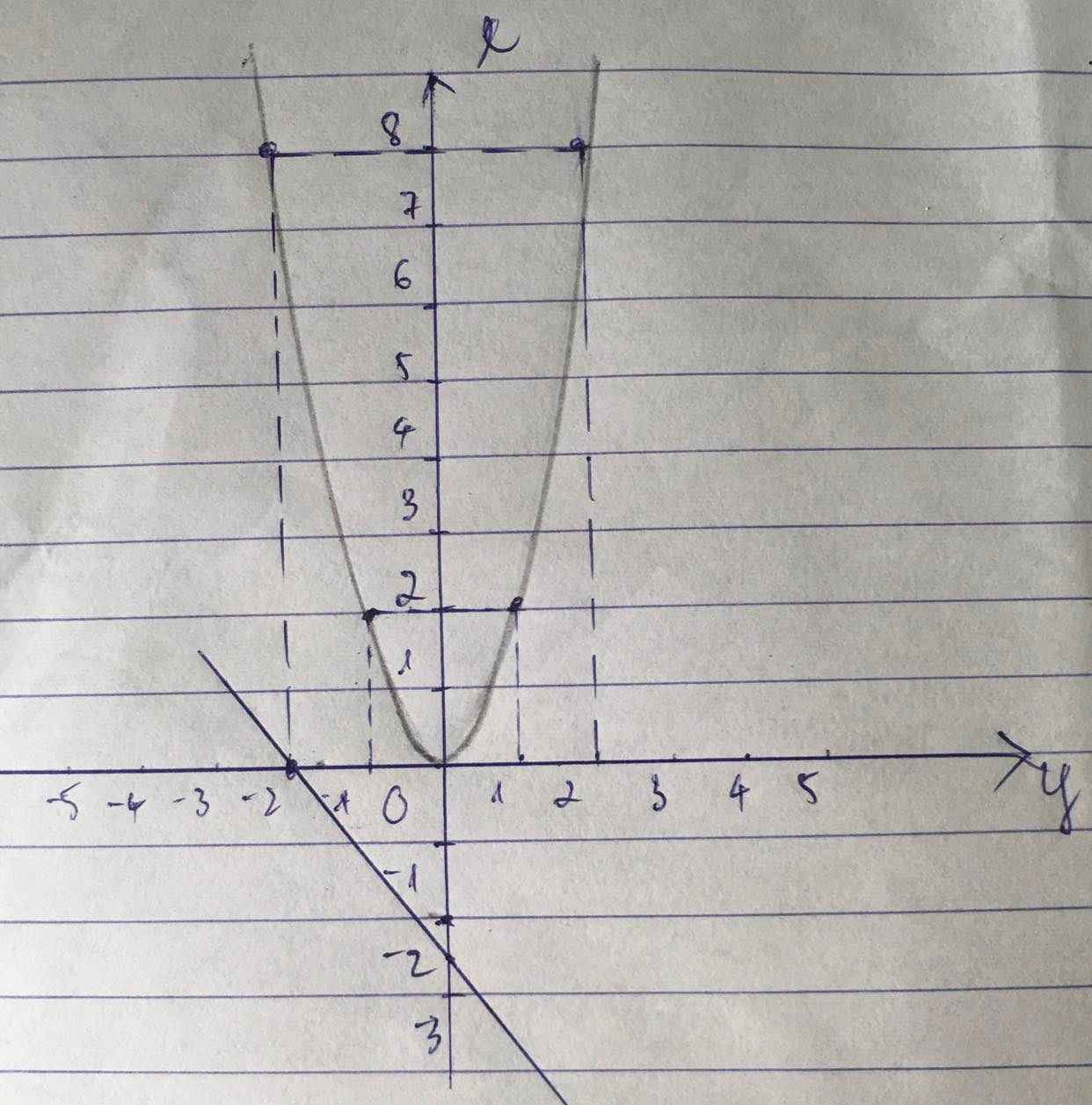
\(y=\left(-2-3\right)x+\left(-2\right).\\ \Leftrightarrow y=-5x-2.\)
i) + \(y=-5x-2.\)
\(Cho\) \(x=0.\Rightarrow y=-2.\)
\(Cho\) \(y=0.\Rightarrow x=\dfrac{-2}{5}.\)
+ \(y=2x^2.\)
| \(x\) | -2 | -1 | 0 | 1 | 2 |
| \(y=2x^2\) | 8 | 2 | 0 | 2 | 8 |
16 tháng 12 2021
Bài 5:
a: Để đây là hàm số bậc nhất thì m+5<>0
hay m<>-5
DT
0
ĐKXĐ: x>=-3/2
\(2x-3\sqrt{2x+3}-7=0\)
=>\(2x+3-3\sqrt{2x+3}-10=0\)
=>\(2x+3-5\sqrt{2x+3}+2\sqrt{2x+3}-10=0\)
=>\(\sqrt{2x+3}\left(\sqrt{2x+3}-5\right)+2\left(\sqrt{2x+3}-5\right)=0\)
=>\(\left(\sqrt{2x+3}-5\right)\left(\sqrt{2x+3}+2\right)=0\)
=>\(\sqrt{2x+3}-5=0\)
=>\(\sqrt{2x+3}=5\)
=>2x+3=25
=>2x=22
=>\(x=\dfrac{22}{2}=11\)