K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
29 tháng 10 2021
\(\left\{{}\begin{matrix}x=5-y\\y\left(5-y\right)=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1\\y=4\end{matrix}\right.\\\left\{{}\begin{matrix}x=4\\y=1\end{matrix}\right.\end{matrix}\right.\)
28 tháng 1 2022
a) Thay m = -2 vào (P) ta có:
\(y=\left(-2-3\right)x+\left(-2\right).\\ \Leftrightarrow y=-5x-2.\)
i) + \(y=-5x-2.\)
\(Cho\) \(x=0.\Rightarrow y=-2.\)
\(Cho\) \(y=0.\Rightarrow x=\dfrac{-2}{5}.\)
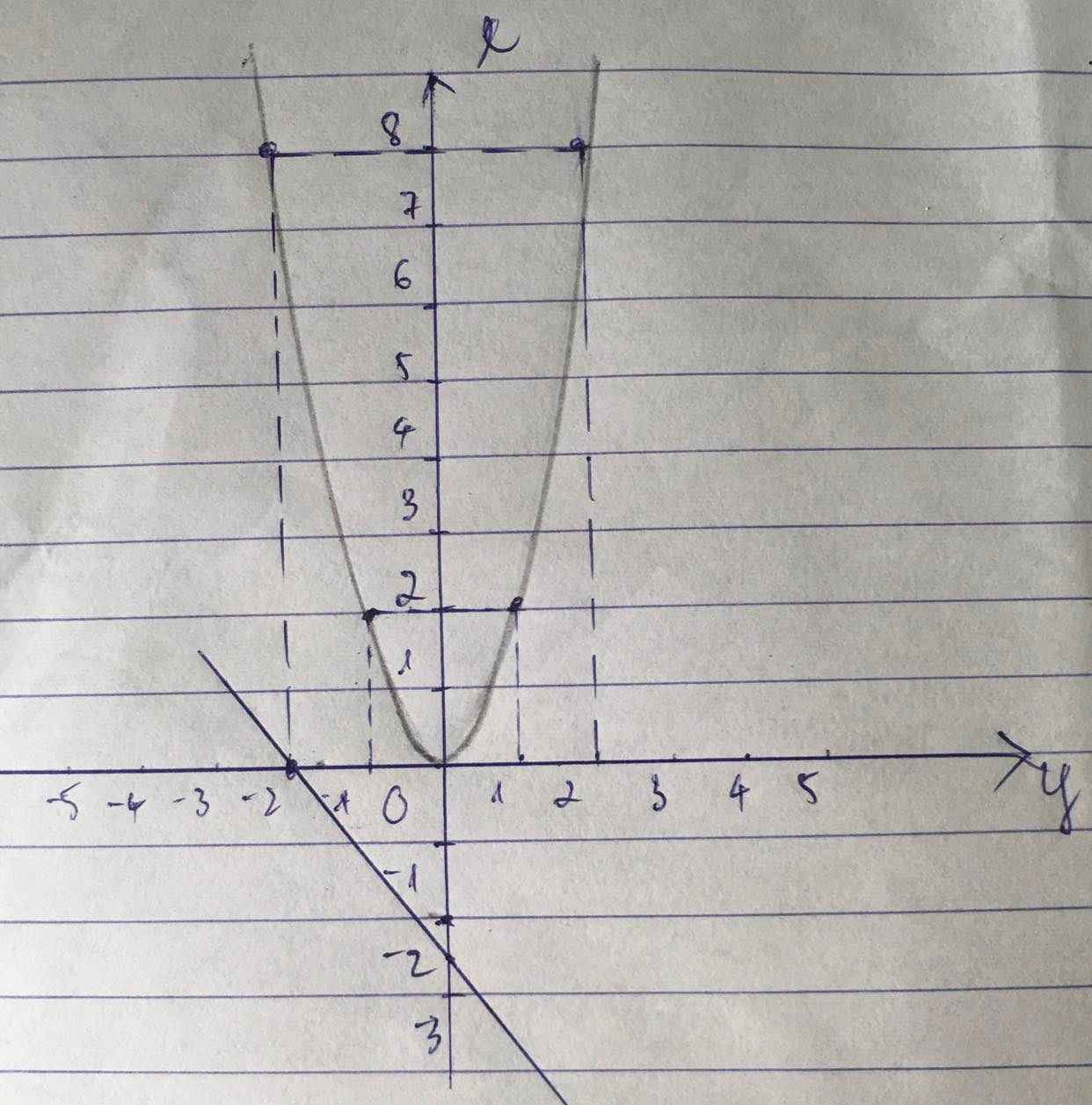
+ \(y=2x^2.\)
| \(x\) | -2 | -1 | 0 | 1 | 2 |
| \(y=2x^2\) | 8 | 2 | 0 | 2 | 8 |
2 tháng 3 2022
1: Thay x=16 vào A, ta được:
\(A=\dfrac{4-1}{4+3}=\dfrac{3}{7}\)
2: \(P=A:B\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+3}:\dfrac{x-3\sqrt{x}-x-6\sqrt{x}-9+x+11\sqrt{x}+6}{x-9}\)
\(=\dfrac{\sqrt{x}-1}{1}\cdot\dfrac{\sqrt{x}-3}{x+2\sqrt{x}-3}=\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\)
24 tháng 11 2021
Bài 2:
\(c,\forall m=0\Leftrightarrow-3x-1=0\Leftrightarrow x=-\dfrac{1}{3}\\ \forall m\ne0\\ \Delta=3^2-4\left(-1\right)\cdot2m^2=8m^2+9>0,\forall m\)
Vậy PT có 2 nghiệm phân biệt với mọi m
16 tháng 12 2021
Bài 5:
a: Để đây là hàm số bậc nhất thì m+5<>0
hay m<>-5
24 tháng 12 2023
ĐKXĐ: x>=-3/2
\(2x-3\sqrt{2x+3}-7=0\)
=>\(2x+3-3\sqrt{2x+3}-10=0\)
=>\(2x+3-5\sqrt{2x+3}+2\sqrt{2x+3}-10=0\)
=>\(\sqrt{2x+3}\left(\sqrt{2x+3}-5\right)+2\left(\sqrt{2x+3}-5\right)=0\)
=>\(\left(\sqrt{2x+3}-5\right)\left(\sqrt{2x+3}+2\right)=0\)
=>\(\sqrt{2x+3}-5=0\)
=>\(\sqrt{2x+3}=5\)
=>2x+3=25
=>2x=22
=>\(x=\dfrac{22}{2}=11\)
12 tháng 11 2023
6:
a: Xét ΔABH vuông tại H có \(cosB=\dfrac{BH}{AB}\)
=>\(cosB=\dfrac{4}{16}=\dfrac{1}{4}\)
Xét ΔABC vuông tại A có \(cosB=\dfrac{BA}{BC}\)
=>\(\dfrac{16}{BC}=\dfrac{1}{4}\)
=>BC=64(cm)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=64^2-16^2=3840\)
=>\(AC=\sqrt{3840}=16\sqrt{15}\left(cm\right)\)
b: Xét ΔABN vuông tại A có AD là đường cao
nên \(BN\cdot BD=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\left(2\right)\)
Từ (1) và (2) suy ra \(BN\cdot BD=BH\cdot BC\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 1 2022
Gọi giá trị của chữ số sau khi xóa đi số 5 là x (với \(x>0;x\in N\))
Giá trị chữ số ban đầu: \(10x+5\)
Theo bài ra ta có pt:
\(10x+5-x=1796\)
\(\Rightarrow9x=1791\)
\(\Rightarrow x=199\)
Vậy chữ số đó là \(1995\)