
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\Leftrightarrow2x=\dfrac{4}{5}-\dfrac{1}{2}=\dfrac{8-5}{10}=\dfrac{3}{10}\)
hay x=3/20
b: \(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{1}{4}=\dfrac{7}{2}\\x-\dfrac{1}{4}=-\dfrac{7}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{15}{4}\\x=-\dfrac{13}{4}\end{matrix}\right.\)
c: \(\Leftrightarrow x^3=-216\)
hay x=-6

\(\dfrac{8^{10}.15^{16}}{12^{15}.25^8}\)
\(=\dfrac{\left(2.4\right)^{10}.\left(3.5\right)^{16}}{\left(3.4\right)^{15}.\left(5^2\right)^8}\)
\(=\dfrac{2^{10}.4^{10}.3^{16}.5^{16}}{3^{15}.4^{15}.5^{16}}\)
\(=\dfrac{2^{10}.3}{4^5}\)
\(=\dfrac{2^{10}.3}{2^{10}}=3\)

có \(a:b:c:d=2:3:4:5\)=> \(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{d}{5}\)=> \(\frac{3a}{6}=\frac{b}{3}=\frac{2c}{8}=\frac{4d}{20}\)
áp dụng tính chất dãy tỉ số bằng nhau, ta co
\(\frac{3a}{6}=\frac{b}{3}=\frac{2c}{8}=\frac{4d}{20}\) =\(\frac{3a+b-2c+4d}{6+3-8+20}\)= \(\frac{105}{21}=5\)
=> 3a= 6.5 = 30, b= 3.5=15, 2c=8.5 =40, 4d= 20.5=100
=> a=10, b= 15, c= 20, d=25
3a+b-2c+4d=105=> 3a+b+4d=105+2c
\(a:b:c:d=2:3:4:5\Rightarrow\frac{a}{2}=\frac{b}{2}=\frac{c}{4}=\frac{d}{5}\)\(\Leftrightarrow\frac{3a}{6}=\frac{b}{3}=\frac{2c}{8}=\frac{4d}{20}\)
\(Vì3a+b+4d=105+2c\Rightarrow3a+b-2c+4d=105\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{3a}{6}=\frac{b}{3}=\frac{2c}{8}=\frac{4d}{20}=\frac{3a+b-2c+4d}{6+3-8+20}\)\(=\frac{105}{21}=5\)
Khi đó \(\frac{3a}{6}=5\Rightarrow a=10\)
\(\frac{b}{3}=5\Rightarrow b=15\)
\(\frac{2c}{8}=5\Rightarrow c=20\)
\(\frac{4d}{20}=5\Rightarrow d=25\)
Vậy a=10;b=15;c=20;d=25

a: Xét ΔABH và ΔACH có
AB=AC
AH chung
BH=CH
Do đó: ΔABH=ΔACH
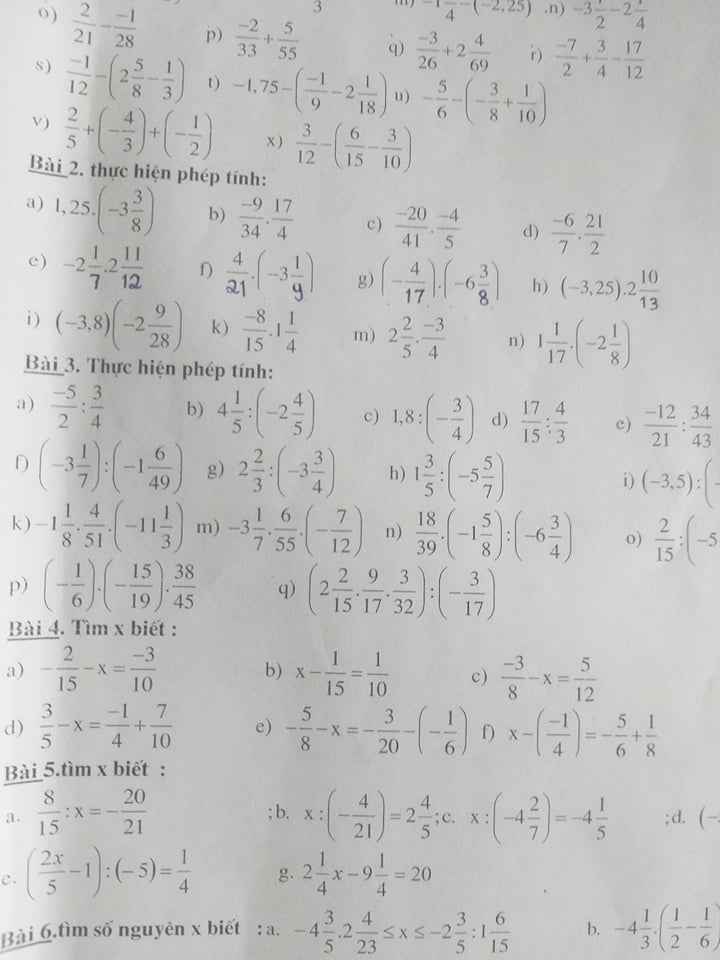 Hơi nhiều bài m.n giải gúp mình nha
Hơi nhiều bài m.n giải gúp mình nha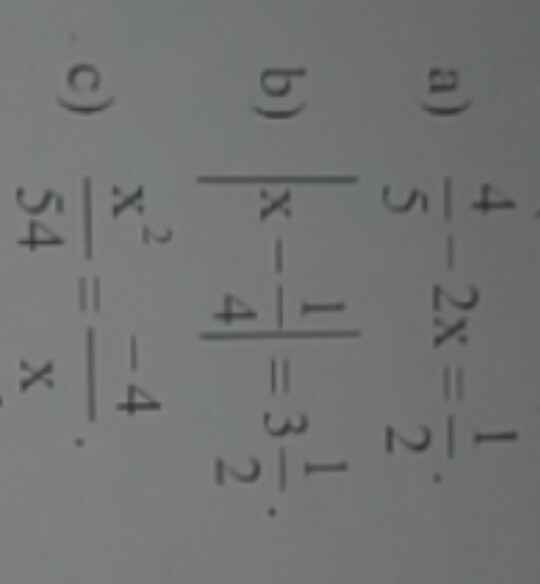
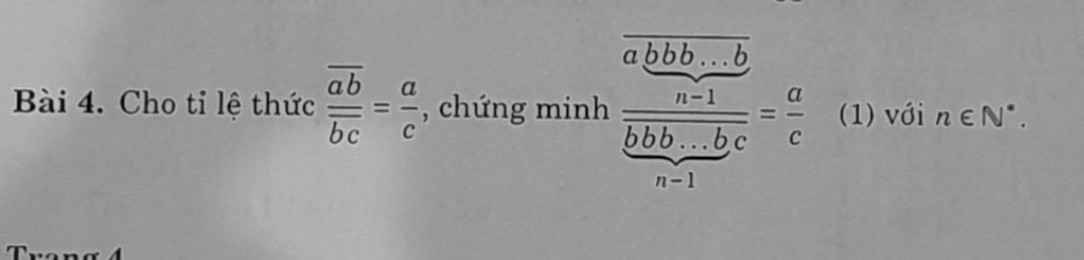
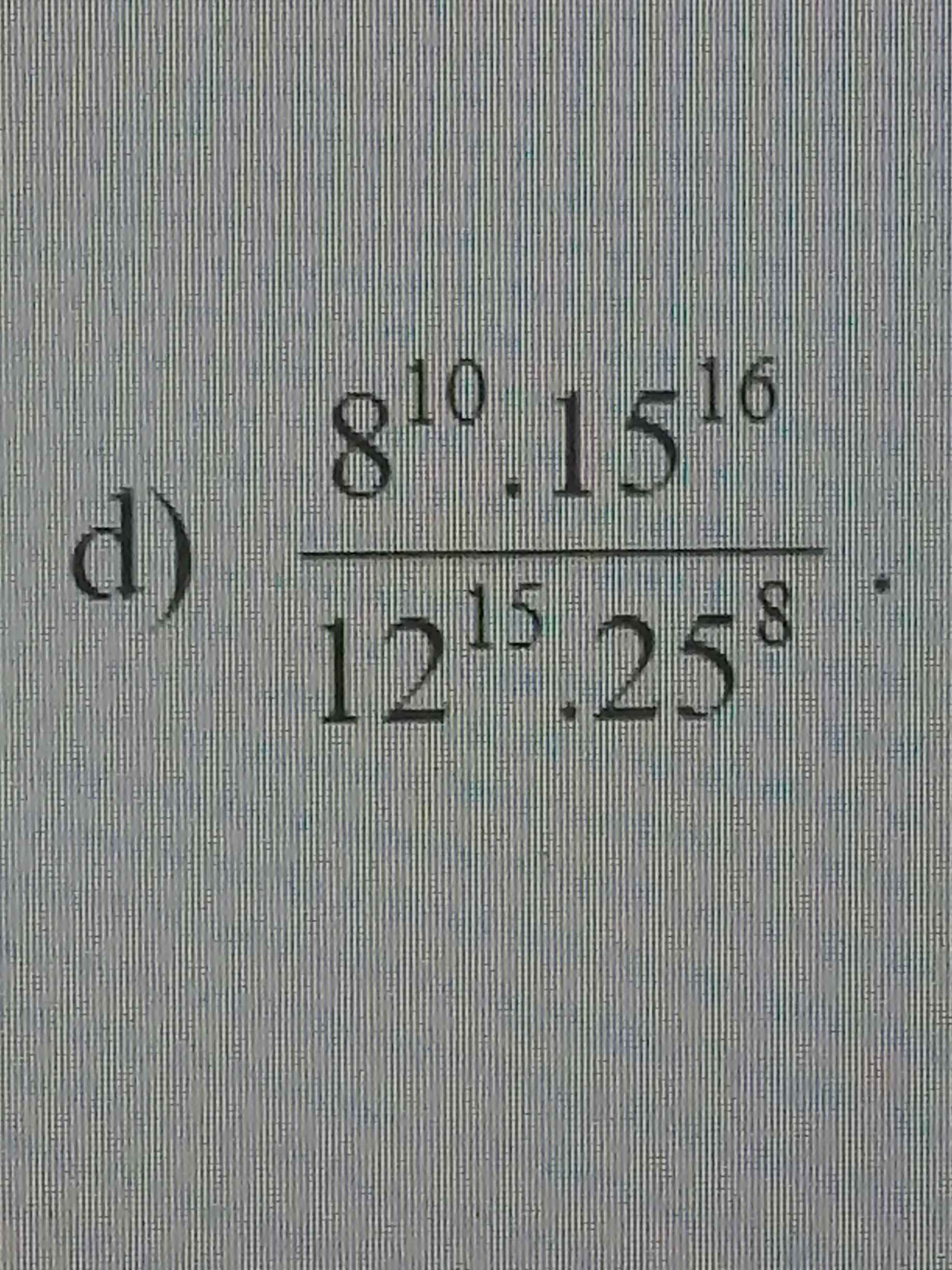
Bài 5:
a: \(\dfrac{8}{15}:x=\dfrac{-20}{21}\)
\(\Leftrightarrow x=\dfrac{-8}{15}\cdot\dfrac{21}{20}=\dfrac{-168}{300}=\dfrac{-14}{25}\)
c: \(x:\left(-4\dfrac{2}{7}\right)=-4\dfrac{1}{5}\)
\(\Leftrightarrow x=\dfrac{-21}{5}\cdot\dfrac{-30}{7}=3\cdot6=18\)