K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
28 tháng 5 2019
Chọn B.
Phương pháp:
Đưa phương trình về dạng tích, giải phương trình tìm nghiệm và tìm điều kiện để bài toán thỏa.
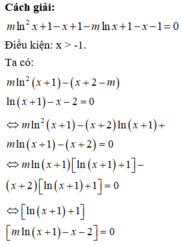
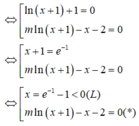

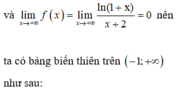
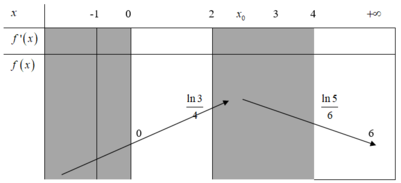


CM
30 tháng 6 2017
Đáp án A
Phương pháp: Chia cả 2 vế cho 3x, đặt  , tìm điều kiện của t.
, tìm điều kiện của t.
Đưa về bất phương trình dạng ![]()
Cách giải :
![]()

Ta có 

Đặt  , khi đó phương trình trở thành
, khi đó phương trình trở thành
![]()

![]()
![]()
![]()
![]()
Ta có: 



Vậy 
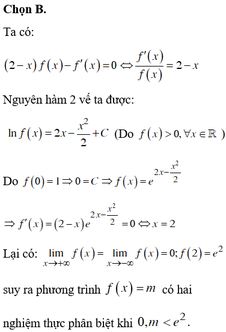
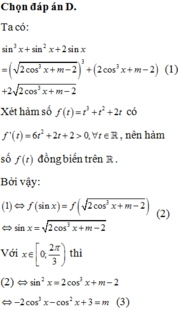





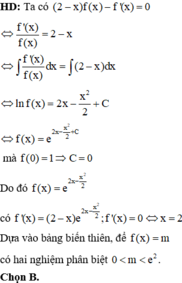

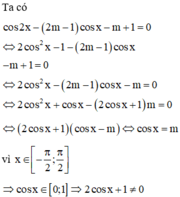

Đáp án B
Điều kiện x 2 − 1 ≥ 0 ⇒ x ≤ − 1 x ≥ 1 .
Phương trình đã cho tương đương với:
2 x 2 − 1 log 2 x 2 + 1 − 2 m 2 x 2 − 1 . log x 2 + 1 + 2 m + 8 = 0
⇔ 2 x 2 − 1 . log x 2 + 1 2 − 2 m 2 x 2 − 1 . log x 2 + 1 + 2 m + 8 = 0 *
Đặt t = x 2 ≥ 1 , theo bài ra ta có
1 ≤ x 1 < x 2 ≤ 3 ⇔ 1 ≤ x 1 2 < x 2 2 ≤ 9 ⇒ t ∈ 1 ; 9 .
Xét hàm số f t = 2 − t − 1 . log t + 1 trên đoạn 1 ; 9 .
Ta có f ' t = log t + 1 2 t − 1 + 2 t − 1 t + 1 . ln 10 > 0, ∀ ∈ 0 ; 9 ⇒ Hàm số f t đồng biến trên đoạn 1 ; 9 . Khi đó f 1 ≤ f t ≤ 9 hay 0 ≤ f t ≤ 4 .
Đặt u = 2 x 2 − 1 . log x 2 + 1 ⇒ u ∈ 0 ; 4 . Khi đó phương trình (*) trở thành u 2 − 2 m . u + 2 m + 8 = 0 1 .
Nhận thấy u=1 không phải là nghiệm của phương trình (1). Với u ≠ 1 thì phương trình (1) tương đương với
u 2 + 8 = 2 m u − 1 ⇔ 2 m = u 2 + 8 u − 1 2
Xét hàm số g u = u 2 + 8 u − 1 trên đoạn 0 ; 4 \ 1 .
Ta có g ' u = u 2 − 2 u − 8 u − 1 2 ; g ' u = 0 ⇔ u = 4 u = − 2 . Mà u ∈ 0 ; 4 \ 1 nên u=4.
Mặt khác, có g 0 = − 8 ; g 4 = 8 ; lim x → 1 − g u = − ∞ ; lim x → 1 + g u = + ∞ .
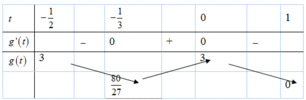
Bảng biến thiên:
Yêu cầu bài toán <=>Phương trình (2) có nghiệm duy nhất trên đoạn 0 ; 4 \ 1 . Suy ra 2 m ≥ 8 2 m ≤ − 8 ⇔ m ≥ 4 m ≤ − 4 .
Mặt khác m ∈ ℤ , m ∈ − 2017 ; 2017 nên suy ra 4 ≤ m ≤ 2017 − 2017 ≤ m ≤ − 4 .
Vậy có tất cả 2017 − 4 + 1 + − 4 + 2017 + 1 = 4028 giá trị m nguyên thỏa mãn bài toán.