
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


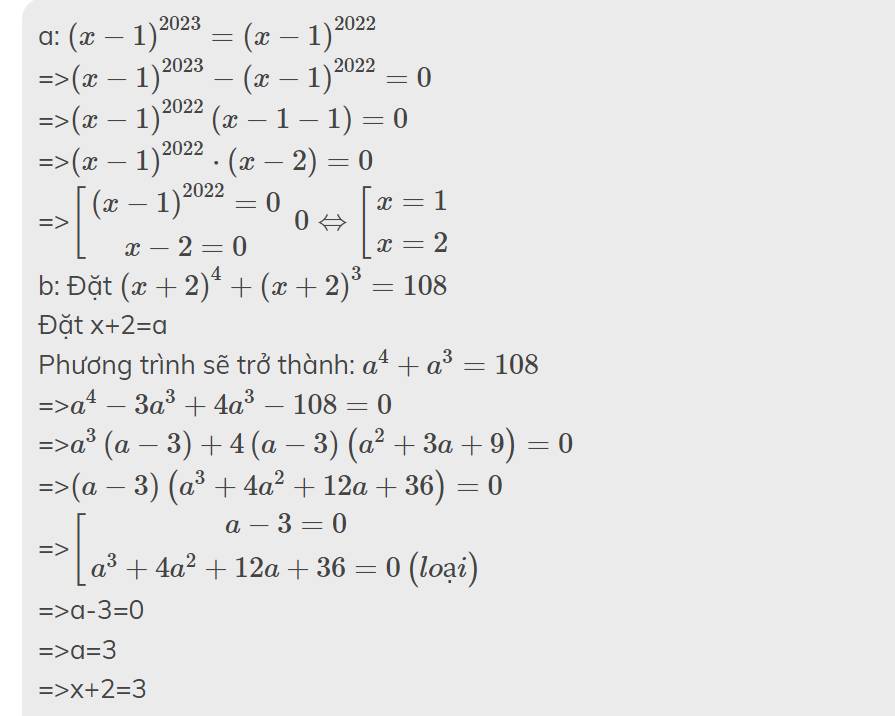
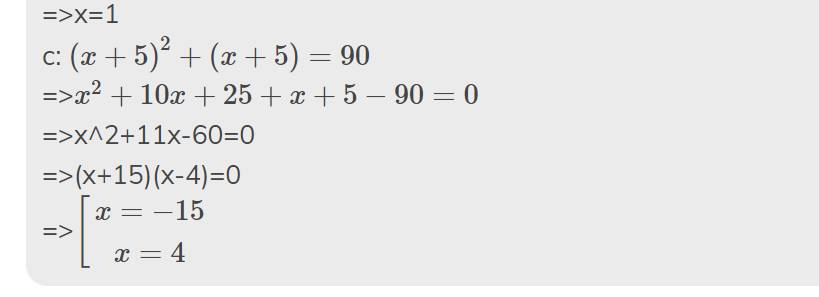
Câu b thì bạn đặt ẩn là bằng x+2 bởi vì nếu khai triển như bình thường thì sẽ là phương trình bậc 4 thì rất khó giải
Câu c thì bạn khai triển theo hằng đẳng thức \(\left(a+b\right)^2=a^2+2ab+b^2\) và sau đó giải như bình thường

a: \(\left(x-1\right)^{2023}=\left(x-1\right)^{2022}\)
=>\(\left(x-1\right)^{2023}-\left(x-1\right)^{2022}=0\)
=>\(\left(x-1\right)^{2022}\left(x-1-1\right)=0\)
=>\(\left(x-1\right)^{2022}\cdot\left(x-2\right)=0\)
=>\(\left[{}\begin{matrix}\left(x-1\right)^{2022}=0\\x-2=0\end{matrix}\right.0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
b: Đặt \(\left(x+2\right)^4+\left(x+2\right)^3=108\)
Đặt x+2=a
Phương trình sẽ trở thành: \(a^4+a^3=108\)
=>\(a^4-3a^3+4a^3-108=0\)
=>\(a^3\left(a-3\right)+4\left(a-3\right)\left(a^2+3a+9\right)=0\)
=>\(\left(a-3\right)\left(a^3+4a^2+12a+36\right)=0\)
=>\(\left[{}\begin{matrix}a-3=0\\a^3+4a^2+12a+36=0\left(loại\right)\end{matrix}\right.\)
=>a-3=0
=>a=3
=>x+2=3
=>x=1
c: \(\left(x+5\right)^2+\left(x+5\right)=90\)
=>\(x^2+10x+25+x+5-90=0\)
=>x^2+11x-60=0
=>(x+15)(x-4)=0
=>\(\left[{}\begin{matrix}x=-15\\x=4\end{matrix}\right.\)

`1)a)5/9 + (-2)/9 = (5+(-2))/9 = 3/9 = 1/3`
`b)(-5)/9 : 10/3 = (-5)/9 . 3/10 = (-5.3)/(9.10) = (-15)/90 = (-1)/6`
`c)(-5)/4 + (-1)/3 +5/4 = (-5/4 + 5/4) + (-1)/3 = 0 + (-1)/3 = -1/3`
`d)(-2)/7 . 5/6 + (-2)/7 . 5/6 = (-2)/7 . ( 5/6 + 5/6 ) = (-2)/7 . 10/6 = (-2)/7 . 5/3 = (-2.5)/(7.3) = (-10)/24 = (-5)/12`
Gì đây mới câu 1 thôi, Còn câu 2,3,4,5 trên bài đâu, giải nhanh đây trước 14h05 trong ngày hôm nay nha.


`Answer:`
Gọi \(ƯC\left(2n+7;5n+17\right)=d\left(d\inℤ\right)\)
\(\Rightarrow\hept{\begin{cases}2n+7⋮d\\5n+17⋮d\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}5\left(2n+7\right)⋮d\\2\left(5n+17\right)⋮d\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}10n+35⋮d\\10n+34⋮d\end{cases}}\)
Lập hiệu: \(\left(10n+35\right)-\left(10n+34\right)\)
\(=10n+35-10n-34\)
\(=\left(10n-10n\right)+\left(35-34\right)\)
\(=1\)
\(\Rightarrow1⋮d\Rightarrow d\inƯ\left(1\right)=\left\{\pm1\right\}\)
Vậy phân số `\frac{2n+7}{5n+17}` tối giản với mọi `n\inNN`
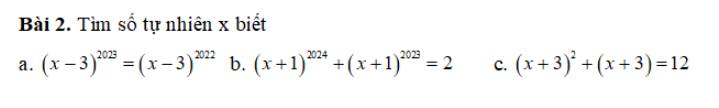
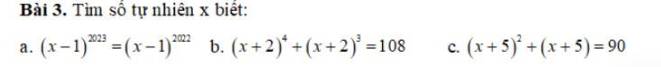
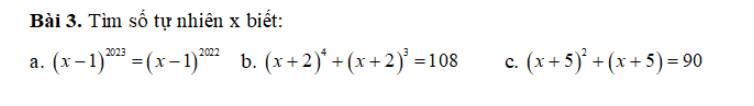



viết chữ xấu nên mình ko đọc dc