Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
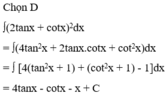
Câu 1: Xét trên miền [1;4]
Do \(f\left(x\right)\) đồng biến \(\Rightarrow f'\left(x\right)\ge0\)
\(x\left(1+2f\left(x\right)\right)=\left[f'\left(x\right)\right]^2\Leftrightarrow x=\frac{\left[f'\left(x\right)\right]^2}{1+2f\left(x\right)}\Leftrightarrow\frac{f'\left(x\right)}{\sqrt{1+2f\left(x\right)}}=\sqrt{x}\)
Lấy nguyên hàm 2 vế:
\(\int\frac{f'\left(x\right)dx}{\sqrt{1+2f\left(x\right)}}=\int\sqrt{x}dx\Leftrightarrow\int\left(1+2f\left(x\right)\right)^{-\frac{1}{2}}d\left(f\left(x\right)\right)=\int x^{\frac{1}{2}}dx\)
\(\Leftrightarrow\sqrt{1+2f\left(x\right)}=\frac{2}{3}x\sqrt{x}+C\)
Do \(f\left(1\right)=\frac{3}{2}\Rightarrow\sqrt{1+2.\frac{3}{2}}=\frac{2}{3}.1\sqrt{1}+C\Rightarrow C=\frac{4}{3}\)
\(\Rightarrow\sqrt{1+2f\left(x\right)}=\frac{2}{3}x\sqrt{x}+\frac{4}{3}\)
Đến đây có thể bình phương chuyển vế tìm hàm \(f\left(x\right)\) chính xác, nhưng dài, thay luôn \(x=4\) vào ta được:
\(\sqrt{1+2f\left(4\right)}=\frac{2}{3}4.\sqrt{4}+\frac{4}{3}=\frac{20}{3}\Rightarrow f\left(4\right)=\frac{\left(\frac{20}{3}\right)^2-1}{2}=\frac{391}{18}\)
Câu 2:
Diện tích hình phẳng cần tìm là hai miền đối xứng qua Oy nên ta chỉ cần tính trên miền \(x\ge0\)
Hoành độ giao điểm: \(sinx=x-\pi\Rightarrow x=\pi\)
\(S=2\int\limits^{\pi}_0\left(sinx-x+\pi\right)dx=4+\pi^2\Rightarrow\left\{{}\begin{matrix}a=4\\b=1\end{matrix}\right.\)
\(\Rightarrow2a+b^3=9\)
a)\(\int \sin ^2\left (\frac{x}{2}\right)dx=\int \frac{1-\cos x }{2}dx=\frac{x}{2}-\frac{\sin x}{2}+c\)
b)\(\int \cos ^2 \left (\frac{x}{2}\right)dx=\int \frac{1+\cos x}{2}dx=\frac{x}{2}+\frac{\sin x}{2}+c\)
c) \(\int \frac{(2x+1)dx}{x^2+x+5}=\int \frac{d(x^2+x+5)}{x^2+x+5}=ln(x^2+x+5)+c\)
d)\(\int (2\tan x+ \cot x)^2dx=4\int \tan ^2 x+\int \cot^2 x+4\int dx=4\int \frac{1-\cos^2 x}{\cos^2 x}dx+\int \frac{1-\sin^2 x}{\sin^2 x}dx+4\int dx \)\( =4\int d(\tan x)-\int d(\cot x)-\int dx=4\tan x-\cot x-x+c\)
Ta có: y = c o t x - 2 c o t x - m
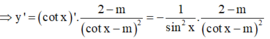
Để hàm số nghịch biến trên khoảng π 4 ; π 2 ⇔ y ' < 0 ; ∀ x ∈ π 4 ; π 2 ( * )
Mà
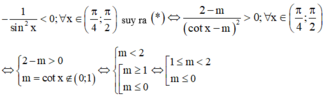
Vậy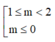 
là giá trị cần tìm.
Chọn B.
\(f\left(x\right)=\dfrac{x^2-1}{x^2}=1-\dfrac{1}{x^2}\)
\(\int f\left(x\right)dx=\int\left(1-\dfrac{1}{x^2}\right)dx=\int1dx-\int x^{-2}dx\)
=\(x-\dfrac{x^{-2+1}}{-2+1}+C=x-\dfrac{x^{-1}}{-1}+C=x+\dfrac{1}{x}+C\)
C=-1 ta được phương án A(ko tm câu hỏi)
C=0 ta được phương án B(ko tm câu hỏi)
C=2 ta được phương án C(ko tm câu hỏi)
=>chọn D
Lời giải:
Ta có: \(y'=\frac{1}{\cos ^2x}-\frac{1}{\sin ^2x}=\frac{\sin ^2x-\cos^2x}{\sin ^2x\cos^2x}=\frac{1-2\cos^2x}{\sin ^2x\cos^2x}\)
Với \(x\in \left(0,\frac{\pi}{2}\right)\) ta chia làm hai đoạn:
+) \(x\in \left(0,\frac{\pi}{4}\right] \Rightarrow 1-2\cos^2x\leq 0\), hàm là hàm nghịch biến
+) \(x\in \left[\frac{\pi}{4},\frac{\pi}{2}\right)\Rightarrow 1-2\cos^2x\geq 0\), hàm là hàm đồng biến
