
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 2:
\(1.f\left(x\right)=2x^3+x^2-3x+9.\\ g\left(x\right)=-2x^3-x^2+3.\)
Câu 3:
1. Ta có: \(AB=AC\) (\(\Delta ABC\) cân).
Mà \(AC=IC\left(gt\right). \)
\(\Rightarrow AB=IC.\)
Ta có: \(\widehat{ABC}=\widehat{ACB}\) (\(\Delta ABC\) cân).
Mà \(\widehat{ACB}=\widehat{ICE}\) (đối đỉnh).
\(\Rightarrow\widehat{ABC}=\widehat{ICE}.\)
Hay \(\widehat{ABD}=\widehat{ICE}.\)
Xét \(\Delta ABD\) và \(\Delta ICE:\)
BD = CE (gt).
\(\widehat{ABD}=\widehat{ICE}\left(cmt\right).\)
AB = IC (cmt).
\(\Rightarrow\Delta ABD=\Delta ICE\left(c-g-c\right).\)
2. Xét \(\Delta BDM\) và \(\Delta CEN:\)
\(\widehat{MBD}=\widehat{NCE}\left(\widehat{ABD}=\widehat{ICE}\right).\)
\(BD=CE\left(gt\right).\)
\(\widehat{BDM}=\widehat{CEN}\left(=90^o\right).\)
\(\Rightarrow\Delta BDM=\Delta CEN\left(g-c-g\right).\)
\(\Rightarrow BM=CN\) (2 cạnh tương ứng).


a)
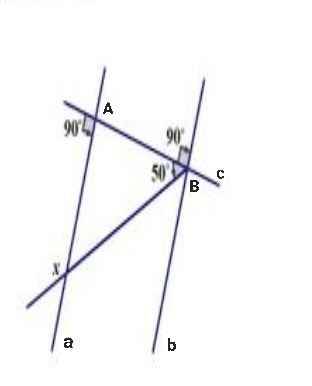 Do a ⊥ c và b ⊥ c
Do a ⊥ c và b ⊥ c
⇒ a // b
Ta có:
∠mBb + ∠ABm = 90⁰
⇒ ∠mBb = 90⁰ - ∠ABm
= 90⁰ - 50⁰
= 40⁰
Mà a // b (cmt)
⇒ ∠aCm = ∠mBb = 40⁰
Ta có:
∠aCm + ∠ACm = 180⁰ (kề bù)
⇒ x = ∠ACm = 180⁰ - ∠aCm
= 180⁰ - 40⁰
= 140⁰
b)
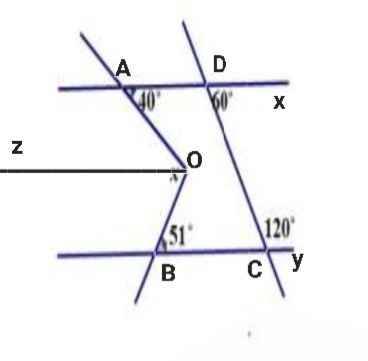 Ta có:
Ta có:
∠ADC + ∠CDx = 180⁰ (kề bù)
⇒ ∠ADC = 180⁰ - ∠CDx
= 180⁰ - 60⁰
= 120⁰
⇒ ∠ADC = ∠DCy = 120⁰
Mà ∠ADC và ∠DCy là hai góc so le trong
⇒ AD // BC
Vẽ tia Oz // AD // BC
Do Oz // AD
⇒ ∠AOz = ∠OAD = 40⁰ (so le trong)
Do Oz // BC
⇒ ∠zOB = ∠OBC = 51⁰ (so le trong)
⇒ x = ∠AOB = ∠AOz + ∠zOB
= 40⁰ + 51⁰
= 91⁰
a,Góc x = 900 + 500 = 1400 (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)
b, Góc x = 510 + 400 = 910

Bài 3.1
a: xét tứ giác ACBD có
O là trung điểm của AB
O là trung điểm của CD
Do đó: ACBD là hình bình hành
Suy ra:AC=DB và AC//DB

Em chia nhỏ bài ra mỗi bài đăng 1 lượt hỏi nha!
Bài 6:
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
=>AM⊥DE

Bài 3:
b: Thay x=-1 vào y=-2x, ta được:
y=-2x(-1)=2
Vậy: B(-1;2) thuộc đồ thị
Bài 2:
b: Thay x=0,5 vào y=-3x, ta được:
y=-3x0,5=-1,5
Vậy: C(0,5;-1,5) thuộc đồ thị

a) \(3\dfrac{1}{4}=\dfrac{2}{3}:\left(\dfrac{-x}{2}\right)\Leftrightarrow\dfrac{13}{4}=\dfrac{2}{3}.\dfrac{-2}{x}\Leftrightarrow\dfrac{-2}{x}=\dfrac{39}{8}\Leftrightarrow x=-\dfrac{16}{39}\)
b) \(1-2\left(x+\dfrac{1}{3}\right)=\left|-\dfrac{2}{3}+\dfrac{1}{5}\right|\Leftrightarrow1-2x-\dfrac{2}{3}=\dfrac{7}{15}\Leftrightarrow2x=-\dfrac{2}{15}\Leftrightarrow x=-\dfrac{1}{15}\)
c) \(\left(2x-1\right)\left(\dfrac{2}{5}-\dfrac{1}{3}x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=0\\\dfrac{2}{5}-\dfrac{1}{3}x=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\\dfrac{1}{3}x=\dfrac{2}{5}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\dfrac{6}{5}\end{matrix}\right.\)
d) \(-4\dfrac{3}{5}.2\dfrac{4}{23}\le x\le-2\dfrac{3}{5}:1\dfrac{6}{15}\Leftrightarrow-10\le x\le-\dfrac{13}{7}\Leftrightarrow x\in\left\{-10;-9;-8;-7;-6;-5;-4;-3;-2;-1\right\}\)(do \(x\in Z\))
Bài 2:
c: Ta có: \(\left(2x-1\right)\left(\dfrac{2}{5}-\dfrac{1}{3}x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=0\\\dfrac{2}{5}-\dfrac{1}{3}x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=1\\\dfrac{1}{3}x=\dfrac{2}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\dfrac{6}{5}\end{matrix}\right.\)


Bài 4:
a: Đặt \(A=\dfrac{1}{2}x^2\left(-2x^2y^2z\right)\cdot\dfrac{-1}{3}x^2y^3\)
\(=\left(\dfrac{1}{2}\cdot\left(-2\right)\cdot\dfrac{-1}{3}\right)\cdot\left(x^2\cdot x^2\cdot x^2\right)\cdot y^5z\)
\(=-\dfrac{1}{3}x^6y^5z\)
bậc là 6+5+1=12
Thay x=-1/2 và y=2 vào A, ta được:
\(A=-\dfrac{1}{3}\cdot\left(-\dfrac{1}{2}\right)^6\cdot2^5\cdot z=-\dfrac{1}{3}z\cdot\dfrac{1}{2}=-\dfrac{1}{6}z\)
b: Đặt \(B=\left(-x^2y\right)^3\cdot\dfrac{1}{2}x^2y^3\cdot\left(-2xy^2z\right)^2\)
\(=-x^6y^3\cdot\dfrac{1}{2}x^2y^3\cdot4x^2y^4z^2\)
\(=-2x^{10}y^{10}z^2\)
Bậc là 10+10+2=22
Thay x=-1/2 và y=2 vào B, ta được:
\(B=-2\cdot\left(-\dfrac{1}{2}\right)^{10}\cdot2^{10}\cdot z^2=-2z^2\)
c: Đặt \(C=\left(-6x^3yz\right)\cdot\left(\dfrac{2}{3}x^2y\right)^2\)
\(=-6x^3yz\cdot\dfrac{4}{9}x^4y^2\)
\(=-\dfrac{8}{3}x^7y^3z\)
bậc là 7+3+1=11
Thay x=-1/2 và y=2 vào C, ta được:
\(C=-\dfrac{8}{3}\cdot\left(-\dfrac{1}{2}\right)^7\cdot2^3\cdot z=\dfrac{1}{6}z\)

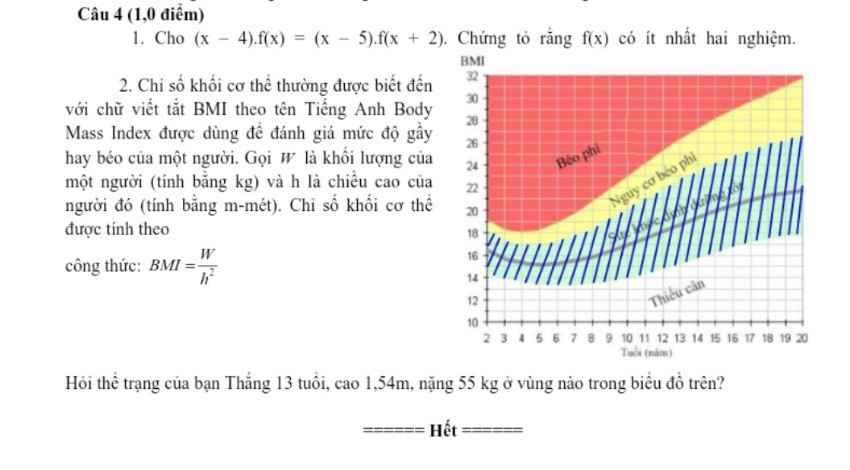 giải hộ mình nhé
giải hộ mình nhé






a: Xét ΔAHB vuông tại H và ΔAHC vuôngtại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: BH=CH=căn 5^2-3^2=4cm
c: Xét ΔABO vuông tại B và ΔACO vuông tại C có
AO chung
AB=AC
=>ΔABO=ΔACO
=>OB=OC
mà AB=AC
nên AO là trung trực của BC
=>A,H,O thẳng hàng