
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các câu hỏi dưới đây có thể giống với câu hỏi trên

TT
20 tháng 4 2017
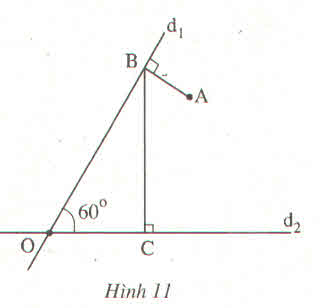
vẽ góc d1Od2 bằng 60 độ
lấy A bất kì nằm trong góc d1Od2
kẻ AB vuông góc với d1O tại B
từ B kẻ BC vuông góc với Od2 tại C
TN
22 tháng 6 2017

Cách vẽ: Vẽ đường thẳng d1 và d2 cắt nhau tại O sao cho \(\widehat{d_1Od_2=60^0}\).Vẽ A nằm trong \(\widehat{d_1}Od_2\) .Qua A ,vẽ đoạn thẳng AB vuông góc với đường thẳng d1 tại điểm B. Qua B, vẽ đoạn thẳng BC vuông góc với đường thẳng d2 tại C.
SG
3

18 tháng 4 2017

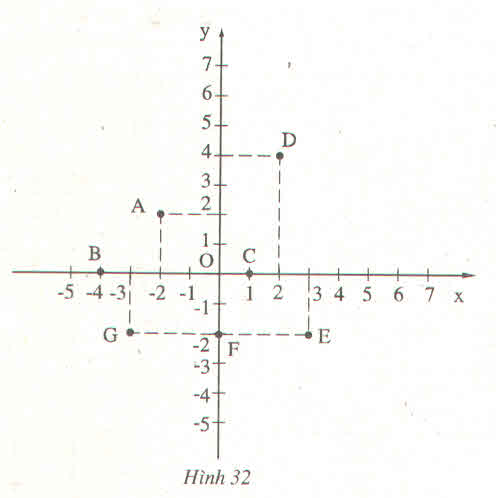
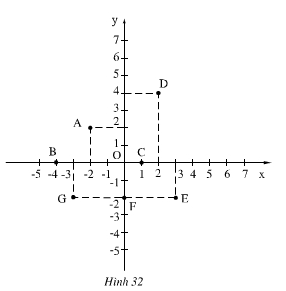
Ta có tọa độ các điểm: A(-2; 2); B(-4; 0); C(1; 0); D(2; 4); E(3; -2); F(0; -2); G(-3; -2)
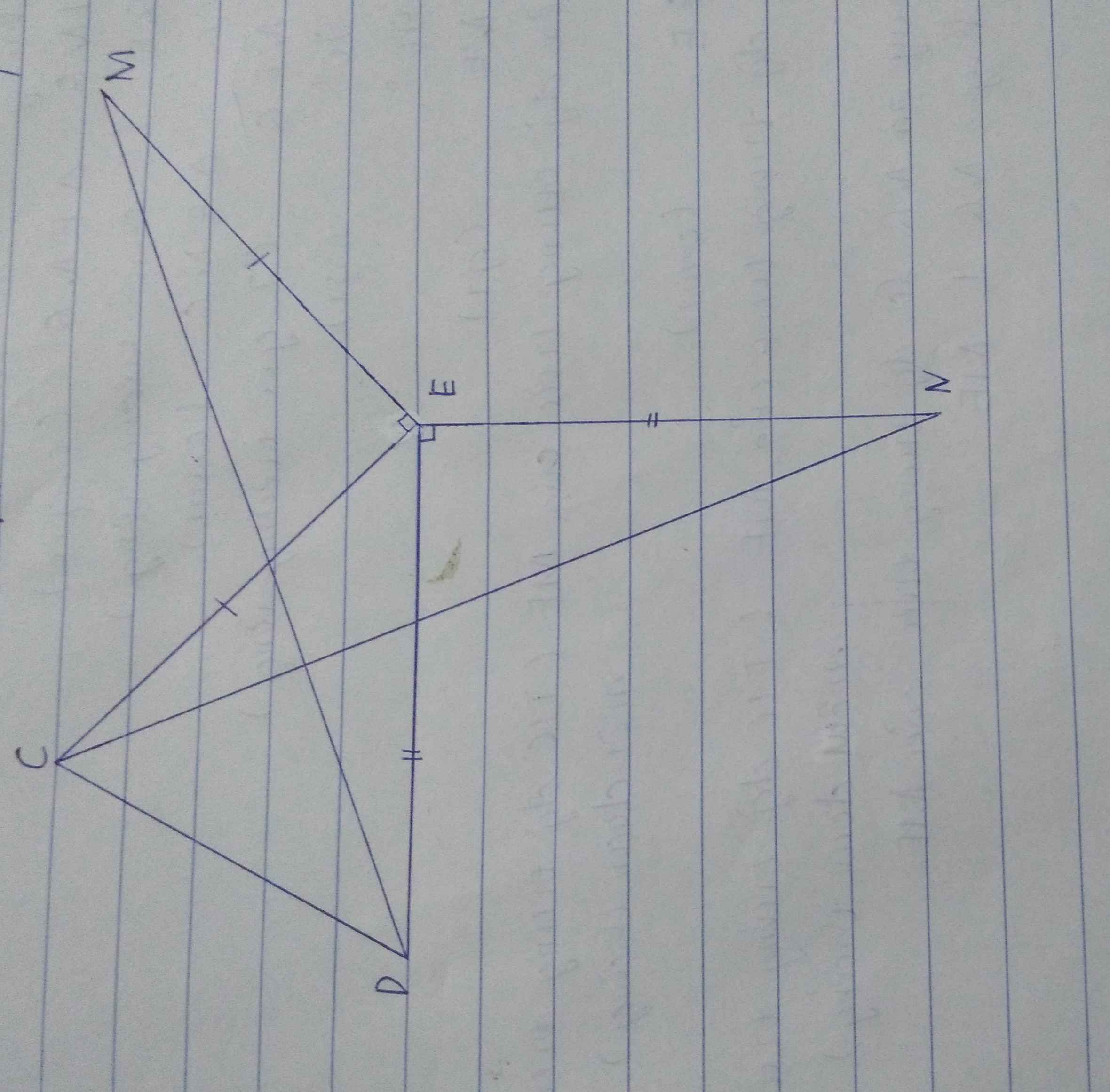














a) Dễ dàng c/m đc tam giác MED = tam giác CEN
=> MD = CN (2 cạnh tương ứng)
b) Gọi O là giao điểm của CE và DM
Tam giác MED = tam giác CEN
=> Góc EMD = Góc ECN (2 góc tương ứng)
Mà: \(\left\{{}\begin{matrix}\widehat{EOM}=\widehat{COD}\left(đối-đỉnh\right)\\\widehat{EOM}+\widehat{EMD}=90^0\end{matrix}\right.\)
=> Góc ECN + Góc COD = 90o
=> Góc COM = 90o
=> MD vuông góc CN
a) Ta chứng minh đc tam giác MED = tam giác CEN
=> MD = CN (2 cạnh tương ứng)
b) Gọi O là giao điểm của CE và DM
Tam giác MED = tam giác CEN
=> Góc EMD = Góc ECN (2 góc tương ứng)
Mà: {ˆEOM=ˆCOD(đối−đỉnh)ˆEOM+ˆEMD=900{EOM^=COD^(đối−đỉnh)EOM^+EMD^=900
=> Góc ECN + Góc COD = 90o
=> Góc COM = 90o
=> MD vuông góc CN