Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(AB=\dfrac{BH}{\sin A}=\dfrac{1,5}{\sin30^0}=3\left(cm\right)\)
Do đó \(P_{ABCD}=4AB=12\left(cm\right)\)

Chu vi hình thoi bằng 16(cm) nên độ dài một cạnh bằng:
16 : 4 = 4(cm)
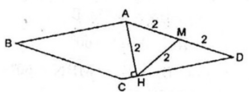
Gọi M là trung điểm của AD.
*Trong tam giác vuông AHD ta có HM là trung tuyến thuộc cạnh huyền, suy ra: HM = AM = 1/2 AD = 1/2 . 4 = 2(cm)
⇒ AM = HM = AH = 2cm
⇒ ∆ AHM đều
⇒ ∠ (HAM ) = 60 0
*Trong tam giác vuông AHD, ta có:
∠ (HAD) + ∠ D = 90 0
⇒ ∠ D = 90 0 - ∠ (HAD) = 90 0 – 60 0 = 30 0
⇒ ∠ B = ∠ D = 30 0 ( t/chất hình thoi)
∠ B + ∠ C = 180 0 ( hai góc trong cùng phía bù nhau)
⇒ ∠ C = 180 0 - ∠ B = 180 0 – 30 0 = 150 0
⇒ ∠ A = ∠ C = 150 0 ( tính chất hình thoi).


