
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tam giác \(ABD\)vuông tại \(A\):
\(BD^2=AB^2+AD^2\)(định lí Pythagore)
\(=4^2+10^2=116\)
\(\Rightarrow BD=\sqrt{116}=2\sqrt{29}\left(cm\right)\)
Lấy \(E\)thuộc \(CD\)sao cho \(AE\perp AC\)
Suy ra \(ABDE\)là hình bình hành.
\(AE=BD=2\sqrt{29}\left(cm\right),DE=AB=4\left(cm\right)\).
Xét tam giác \(AEC\)vuông tại \(A\)đường cao \(AD\):
\(\frac{1}{AD^2}=\frac{1}{AE^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{AC^2}=\frac{1}{AD^2}-\frac{1}{AE^2}=\frac{1}{100}-\frac{1}{116}=\frac{1}{715}\)
\(\Rightarrow AC=\sqrt{715}\left(cm\right)\)
\(AE^2=ED.EC\Leftrightarrow EC=\frac{AE^2}{ED}=\frac{116}{4}=29\left(cm\right)\)suy ra \(DC=25\left(cm\right)\)
Hạ \(BH\perp CD\).
\(BC^2=HC^2+BH^2=21^2+10^2=541\Rightarrow BC=\sqrt{541}\left(cm\right)\)
\(S_{ABCD}=\left(AB+CD\right)\div2\times AD=\frac{4+25}{2}\times10=145\left(cm^2\right)\)

Ta có: \(AH^2=HD.HB=18.8=144\Rightarrow AH=12\) (cm)
\(\Rightarrow AD=\sqrt{AH^2+HD^2}=\sqrt{12^2+18^2}=6\sqrt{13}\)
\(AB=\sqrt{12^2+8^2}=4\sqrt{13}\)
Ta có: \(DH^2=HA.HC\Rightarrow CH=\dfrac{DH^2}{HA}=\dfrac{18^2}{12}=27\)
\(\Rightarrow CD=\sqrt{CH^2+HD^2}=\sqrt{27^2+18^2}=9\sqrt{13}\)
\(\Rightarrow S_{ABCD}=\dfrac{1}{2}\left(AB+CD\right).AD=\dfrac{1}{2}\left(4\sqrt{13}+9\sqrt{13}\right).6\sqrt{13}\)
\(=507\left(cm^2\right)\)

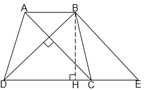
Qua B vẽ đường thẳng song song với AC, cắt DC ở E. Gọi BH là đường cao của hình thang. Ta có BE // AC, AC ⊥ BD nên BE ⊥ BD
Áp dụng định lý Pytago vào tam giác vuông BDH, ta có: B H 2 + H C 2 = B D 2
12 2 + H D 2 = 15 2 ⇒ H D 2 = 81 => HD = 9cm
Xét tam giác BDE vuông tại B:
B D 2 = D E . D H ⇒ 15 2 = D E . 9 ⇒ D E = 25 c m DE = 25cm
Ta có: AB = CE nên AB + CD = CE + CD = DE = 25cm
Do đó S A B C D = 25.12 : 2 = 150( c m 2 )
Đáp án cần chọn là: A

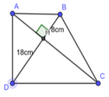
Xét ∆ ADB vuông tại A có: AH là đường cao ứng với cạnh huyền BD
⇒ A H 2 = HB. HD = 8.18 HA = 12 (cm) (hệ thức lượng trong tam giác vuông)
Xét ∆ ADC vuông tại D có: DH là đường cao ứng với cạnh huyền AC
⇒ H D 2 = H A . H C ⇒ 18 2 = 12 H C => HC = 27 (cm) (hệ thức lượng trong tam giác vuông)
Ta có: AC = AH + HC = 12 + 27 = 39 cm
BD = BH + HD = 8 + 18 = 26cm
S A B C D = A C . B D 2 = 26.39 2 = 507 c m 2
Đáp án cần chọn là: D
Do hình thang ABCD có 2 đường chéo vuông góc với nhau nên
SABCD= 1/2 . AC . BD = 1/2 . 6 . 3,6 = 10,8 ( dm2 )
Vậy SABCD = 10,8dm2
Hok tốt