Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nữa chu vi đáy của hình chóp đều:
\(5\cdot4:2=10\left(cm\right)\)
Diện tích xung quanh của hình chóp đều là:
\(S_{xq}=10\cdot6,5=65\left(cm^2\right)\)
Diện tích đáy của hình chóp đều:
\(5^2=25\left(cm^2\right)\)
Thể tích của hình chóp đều:
\(V=\dfrac{1}{3}\cdot25\cdot6=50\left(cm^3\right)\)

Lời giải:
Xét tam giác $SAB$ có $SA=SB=10$, $AB=12$
Kẻ $SH\perp AB$ thì $H$ là trung điểm của $AB$.
$\Rightarrow AH=6$ (cm)
Theo định lý Pitago:
$SH=\sqrt{SA^2-AH^2}=\sqrt{10^2-6^2}=8$ (cm)
$S_{SAB}=\frac{SH.AB}{2}=\frac{8.12}{2}=48$ (cm vuông)
$S_{xq}=3S_{SAB}=3.48=144$ (cm vuông)

a: S.ABC là hình chóp đều
=>SA=SB=SC và AB=AC=BC
ΔSAB cân tại S có SM là trung tuyến
nên SM vuông góc AB
=>ΔSMA vuông tại M
\(MA=\sqrt{SA^2-SM^2}=2\left(cm\right)\)
=>BA=2*2=4cm=BC=AC
b: \(S_{Xq}=\dfrac{1}{2}\left(4+4+4\right)\cdot5=6\cdot5=30\left(cm^2\right)\)
c: \(S_{tp}=30+4^2\cdot\dfrac{\sqrt{3}}{4}=30+4\sqrt{3}\left(cm^2\right)\)


a) Ta có: AC2 = AB2 + BC2 (Pytago) = 32 + 32 = 18(cm)
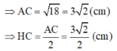
Lại có: SH2 = SC2 - HC2 (Pytago)
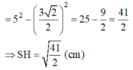
b) Gọi K là trung điểm của BC
Ta có: SK2 = SH2 + HK2 (Pytago)
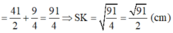
![]()
![]()
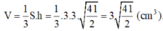

Lời giải:
Nửa chu vi đáy: $5.2=10$ (cm)
Diện tích xung quanh:
$S_{xq}=10.6=60(cm^2)$
Đáp án A.


Kẻ SO vuông góc (ABC)
=>SO là trung đoạn của hình chóp S.ABC và O là tâm của ΔABC
Gọi giao của AO với BC là E
=>AO vuông góc BC tại E
ΔABC đều có AE là đường cao và O là tâm
nên AO=2/3AE và \(AE=\dfrac{6\sqrt{3}}{2}=3\sqrt{3}\left(cm\right)\)
=>\(AO=2\sqrt{3}\left(cm\right)\)
ΔSAO vuông tại O
=>SO^2+OA^2=SA^2
=>\(SO^2+12=5^2\)
=>\(SO=\sqrt{13}\left(cm\right)\)
\(S_{XQ}=\dfrac{1}{2}\sqrt{13}\cdot6\cdot3=9\sqrt{13}\)
=>Không có câu nào đúng