Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vật chuyển động từ trạng thái nghỉ đến vận tốc cực đại \(v_0\)
áp dụng công thức của chuyển động biến đổi đều ta có
\(2a_1s_1=v^2_0\)
Trong quá trình giảm dần đều ta cũng có
\(2a_2s_2=v^2_0\)
Theo đầu bài cho \(s_2=2s_1\) dẫn đến \(a_1=2a_2\)
Và thời gian \(\Delta t_2=2\Delta t_1\)

Gọi khoảng cách giữa hai bến sông là S = AB, giả sử nước chảy từ A đến B với vận tốc u ( u < 3km/h )
- Thời gian thuyền chuyển động từ A đến B là: t1 = \(\frac{S}{v_1+u}\)
- Thời gian chuyển động của ca nô là: t2 = \(\frac{2S}{v_2-u}+\frac{2S}{v_2+u}\)
Theo bài ra: t1 = t2 \(\Leftrightarrow\frac{S}{v_1+u}=\frac{2S}{v_2-u}+\frac{2S}{v_2+u}\)
Hay: \(\frac{1}{v_1+u}=\frac{2}{v_2-u}+\frac{2}{v_2+u}\Rightarrow\)\(u^2+4v_2u+4v_1v_2-v^2_2=0\) \(\left(1\right)\)
Giải phương trình (1) ta được: \(u\approx\text{ - 0,506 km/h }\)
Vậy nước sông chảy theo hướng BA với vận tốc gần bằng 0,506 km/h
b. Nếu nước chảy nhanh hơn thì thời gian ca nô đi về về B (với quãng đường như câu a) có thay đổi không? vì sao?

Toàn bộ năng lượng đến trong 1s là:
\(E_1=N_1\frac{hc}{\lambda_1}\)
Năng lượng hạt phát ra trong 1s là :
\(E_2=N_2\frac{hc}{\lambda_2}\)
mặt khác ta có
\(E_2=H.E_1\)
\(N_2\frac{hc}{\lambda_2}=HN_1\frac{hc}{\lambda_1}\)
\(\frac{N_2}{\lambda_2}=H\frac{N_1}{\lambda_1}\)
\(N_2=H\frac{N_1\lambda_2}{\lambda_1}=2.4144.10^{13}hạt\)

1Bình chọn giảm
Trong trường hợp ban đầu giotj thủy ngân nằm chính giữa nên thể tích 2 phần bằng nhau
Tỉ số này không đổi do khí vẫn được giữ cố định trong bình.
Khi cùng tăng nhiệt độ của 2 bình lên 1 lượng nhỏ thì tỉ số giua 2 nhiệt độ thay đổi dẫn đến tỉ lệ thể tích thay đổi. Bên nào thể tích nhỏ hơn thì là do giotj thủy ngân dịch về phía đó.
Tỷ số giua 2 nhiệt độ phụ thuộc (T1 > T2 hay không)
Nêú biết bên nào có nhiệt độ cao hơn sẽ biết thủy ngân dịch về bên nào

\(U_C=I.Z_C=\dfrac{U.Z_C}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}.\omega C}=\dfrac{U}{\sqrt{\omega^2.C^2.R^2+(\omega^2.LC-1)^2}}\)
Suy ra khi \(\omega=0\) thì \(U_C=U\) \(\Rightarrow (1)\) là \(U_C\)
\(U_L=I.Z_L=\dfrac{U.Z_L}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U.\omega L}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}}=\dfrac{U.L}{\sqrt{\dfrac{R^2}{\omega^2}+(L-\dfrac{1}{\omega^2 C})^2}}\)(chia cả tử và mẫu cho \(\omega\))
Suy ra khi \(\omega\rightarrow \infty\) thì \(U_L\rightarrow U\) \(\Rightarrow (3) \) là \(U_L\)
Vậy chọn \(U_C,U_R,U_L\)

> O x M 7 -7 π/3
Quỹ đạo chuyển động là 14 cm → A = 7 cm.
Tại thời điểm ${t_0}$ chất điểm ở vị trí M có pha ban đầu là –π/3; độ lớn gia tốc cực đại tại biên.
→ từ M đến biên lần thứ 3 thì ∆φ = π/3 + 2π = 7π/3 rad.
→ t = ∆φ/ω = 7/6 s và s = 3,5 + 28 = 31,5 cm
→ v = s/t = 27 cm/s.

Suất điện động hiệu dụng là \(E = \dfrac{{{E_0}}}{{\sqrt 2 }} = \dfrac{{220\sqrt 2 }}{{\sqrt 2 }} = 220V\).
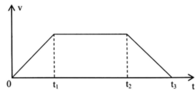

+ Trong khoảng thời gian từ 0 đến t 1 thuộc chuyển động nhanh dần đều (vì vận tốc tăng)
+ Trong khoảng thời gian từ t 1 đến t 2 thuộc chuyển động thẳng đều (vì vận tốc không đổi)
+ Trong khoảng thời gian từ t 2 đến t 3 thuộc chuyển động chậm dần đều (vì vận tốc giảm) => Chọn C