Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
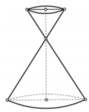
Gọi r , h , r ' , h ' lần lượt là bán kính và chiều cao của hình nón lớn và nhỏ
Phân tích dữ kiện
+) Chiều cao của đồng hồ là 30 cm ⇔ h + h ' = 30 c m
+) Tổng thể tích của đồng hồ là 1000 π c m 3
⇔ V l + V n = π r 2 h + π r ' 2 h ' 3 = 1000 π ⇔ r 2 h + r ' 2 h ' = 3000
+) Đường sinh bất kỳ của hình nón tạo với đáy một góc 60 ° ⇔ h r = h ' r ' = 3
Ta có hệ:
h + h ' = 3 r + r ' r 2 h + r ' 2 h ' = 3 r 3 + r ' 3 = 3000 ⇔ 3 r + r ' 3 = 9000 3 r 3 + r ' 3 = 3000 ⇔ r + r ' 3 r 3 + r ' 3 = 3
⇔ 2 r ' 2 − 5 r r ' + 2 r 2 = 0 ⇔ r r ' = 1 2
vì 0 < r ' < r
Theo đó tỉ lệ cần tính là:
V n V l = r ' 2 h ' r 2 h = r ' r 3 = 1 8

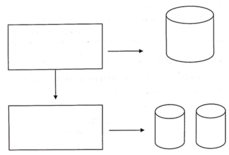
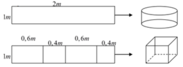
Ban đầu bán kính đáy là R, sau khi cắt và gò ta được 2 khối trụ có bán kính đáy là R 2 . Đường cao của các khối trụ không thay đổi. Ta có:
V 1 = S d h = π . R 2 . h V 2 = 2 S dl . h = 2 π R 2 h = πR 2 h 2
Khi đó: V 1 V 2 = 2
Đáp án C

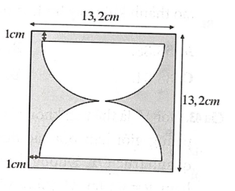
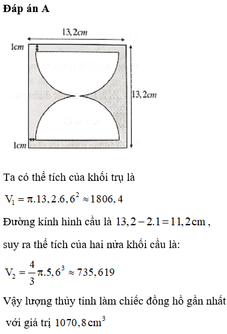
Đáp án A
Phương pháp:
Tính độ dài các đoạn thẳng MN và MQ sau đó áp dụng công thức tình thể tích hình trụ V = π r 2 h


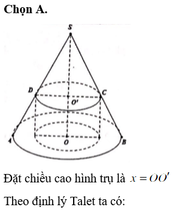
Chọn A
Phương pháp: Sử dụng công thức thể tích hình trụ và công thức thể tích hình hộp.
Cách giải:

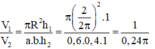

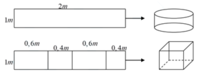

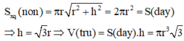
Đáp án đúng : D