K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TM
29 tháng 3 2017
phương trình nghiệm nguyên có nhiều dạng và nhiều cách làm lắm bạn ạ, bạn hỏi cụ thể bài nào để mình còn xem chứ
HP
29 tháng 3 2017
mua quyển "pt nghiệm nguyên và kinh nghiệm giải" ,muốn dạng nào cũng có
17 tháng 1 2021
Câu 4b:
Ta có \(a-\sqrt{a}=\sqrt{b}-b\Leftrightarrow a+b=\sqrt{a}+\sqrt{b}\). (1)
Áp dụng bất đẳng thức Cauchy - Schwarz ta có:
\(a^2+b^2\ge\dfrac{\left(a+b\right)^2}{2};\sqrt{a}+\sqrt{b}\le\sqrt{2\left(a+b\right)}\).
Kết hợp với (1) ta có:
\(a+b\le\sqrt{2\left(a+b\right)}\Leftrightarrow0\le a+b\le2\).
Ta có: \(P\ge\dfrac{\left(a+b\right)^2}{2}+\dfrac{2020}{\left(\sqrt{a}+\sqrt{b}\right)^2}\) (Do \(a^2+b^2\ge\dfrac{\left(a+b\right)^2}{2}\))
\(=\dfrac{\left(a+b\right)^2}{2}+\dfrac{2020}{\left(a+b\right)^2}\) (Theo (1))
\(\Rightarrow P\ge\dfrac{\left(a+b\right)^2}{2}+\dfrac{2020}{\left(a+b\right)^2}\).
Áp dụng bất đẳng thức AM - GM cho hai số thực dương và kết hợp với \(a+b\le2\) ta có:
\(\dfrac{\left(a+b\right)^2}{2}+\dfrac{2020}{\left(a+b\right)^2}=\left[\dfrac{\left(a+b\right)^2}{2}+\dfrac{8}{\left(a+b\right)^2}\right]+\dfrac{2012}{\left(a+b\right)^2}\ge2\sqrt{\dfrac{\left(a+b\right)^2}{2}.\dfrac{8}{\left(a+b\right)^2}}+\dfrac{2012}{2^2}=4+503=507\)
\(\Rightarrow P\ge507\).
Đẳng thức xảy ra khi a = b = 1.
Vậy Min P = 507 khi a = b = 1.
17 tháng 1 2021
Giải nốt câu 4a:
ĐKXĐ: \(x\geq\frac{-1}{2}\).
Phương trình đã cho tương đương:
\(x^2+2x+1=2x+1+2\sqrt{2x+1}+1\)
\(\Leftrightarrow\left(x+1\right)^2=\left(\sqrt{2x+1}+1\right)^2\)
\(\Leftrightarrow\left(x+1\right)^2-\left(\sqrt{2x+1}+1\right)^2=0\)
\(\Leftrightarrow\left(x+1-\sqrt{2x+1}-1\right)\left(x+1+\sqrt{2x+1}+1\right)=0\)
\(\Leftrightarrow\left(x-\sqrt{2x+1}\right)\left(x+\sqrt{2x+1}+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\sqrt{2x+1}=0\left(1\right)\\x+\sqrt{2x+1}+2=0\left(2\right)\end{matrix}\right.\).
Ta thấy \(x+\sqrt{2x+1}+2>0\forall x\ge-\dfrac{1}{2}\).
Do đó phương trình (2) vô nghiệm.
Xét phương trình (1) \(\Leftrightarrow x=\sqrt{2x+1}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x^2=2x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left(x-1\right)^2=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left[{}\begin{matrix}x-1=\sqrt{2}\\x-1=-\sqrt{2}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left[{}\begin{matrix}x=\sqrt{2}+1>0>-\dfrac{1}{2}\left(TM\right)\\x=-\sqrt{2}+1< 0\left(\text{loại}\right)\end{matrix}\right.\end{matrix}\right.\).
Vậy nghiệm của phương trình là \(x=\sqrt{2}+1\).
TP
1
13 tháng 9 2015
\(\text{Với x;y là hai số thực dương ta có: }x+y\ge2\sqrt{xy}\text{ Dấu "=" xảy ra khi x=y }\)
\(\text{Với x;y;z là 3 số thực duong ta có: }x+y+z\ge3\sqrt[3]{xyz}\text{ Dấu "=" xảy ra khi x=y=z}\)
KK
24 tháng 11 2018
Giải:
Gọi tuổi của Thơ, Toán, Thi, Tài là a, b, c, d (a,b,c,d∈N⊛)
Ta có: a=23b⇒a2=b3⇒a8=b12
c=34a⇒c3=a4⇒c6=a8
d=56c⇒d5=c6
⇒a8=b12=c6=d5
Đặt a8=b12=c6=d5=k⇒⎧⎩⎨⎪⎪⎪⎪⎪⎪a=8kb=12kc=6kd=5k
Lại có: a+b+c+d=62
⇒8k+12k+6k+5k=62
⇒31k=62
⇒k=2
⇒⎧⎩⎨⎪⎪⎪⎪⎪⎪a=16b=24c=12d=10
Vậy Thơ 16 tuổi, Toán 24 tuổi, Thi 12 tuổi, Tài 10 tuổi
KK
24 tháng 11 2018
Gọi Tuổi của Thơ; Toán; Thi; Tài lần lượt là a,; b; c; d
Theo bài ra ta có:
+ a=23b (1)
+ c=34a => c=23.34b = 12b (2)
+ d=56c => d=56.12b=512b (3)
Mặt khác: a + b + c + d = 62 (4)
Từ (1); (2); (3); (4)
=> 23b+b+12b+512b=62
=> b(23+1+512+12) = 62
=> 3112b=62
=> b = 62.1231=24
=> a = 23.24=16
c = 12.24 = 12
d = 512.24=10
Vậy tuổi của Thơ là 16 ; Toán là 24; Thi là 12; Tài là 10
TT
0
PT
1
CM
10 tháng 9 2018
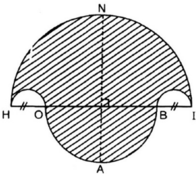
Cách vẽ
- Vẽ nửa đường tròn đường kính HI = 10cm, tâm M.
- Trên đường kính HI lấy điểm O và điểm B sao cho HO = BI = 2cm.
- Vẽ hai nửa đường tròn đường kính HO, BI nằm cùng phía với đường tròn (M).
- Vẽ nửa đường tròn đường kính OB nằm khác phía đối với đường tròn (M). Đường thẳng vuông góc với HI tại M cắt (M) tại N và cắt đường tròn đường kính OB tại A.
chào bạn
có gì vui ko Nguyễn Ngọc Ánh