K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
30 tháng 7 2023
a: DE<EF
=>góc F<góc D
b: Xét ΔDKE vuông tại K và ΔDKI vuông tại K có
DK chung
KE=KI
=>ΔDKE=ΔDKI
c: ΔDKE=ΔDKI
=>DE=DI
=>ΔDEI cân tại D
mà góc DEI=60 độ
nên ΔDEI đều
26 tháng 9 2023
Giá gốc mỗi cái túi:
\(150000:50=3000\left(đồng\right)\)
Số tiền nhận khi bán 30 cái túi:
\(3000\cdot30\cdot130\%=117000\left(đồng\right)\)
Số tiền nhận khi bán 20 cái túi còn lại:
\(3000\cdot20\cdot95\%=57000\left(đồng\right)\)
Tổng tiền mà cửa hàng nhận khi bán hết:
\(117000+57000=174000\left(đồng\right)\)
Vậy là lãi số tiền là:
\(174000-150000=24000\left(đồng\right)\)
Đáp số: lãi 24 000 đồng
26 tháng 9 2023
Giá vốn của 50 chiếc túi sách là:
50 x 150000 = 7500000 đồng
Giá bán để cửa hàng lãi 30% so với giá gốc là:
150000 x ( 100% + 30%) = 195000 đồng
Số tiền thu được khi bán với giá lãi 30% là:
30 x 195000 = 5850000 đồng
Giá bán làm cửa hàng lỗ 5% là:
150000 x ( 100% - 5%) = 142500 đồng
Số tiền thu được khi bán với giá lỗ 5% là:
20 x 142500 = 2850000 đồng
Tổng số tiền thu được là:
5850000 + 2850000 = 8700000 đồng
Cửa hàng đó sẽ lãi số tiền là:
8700000 - 7500000 = 1200000 đồng
KV
20 tháng 10 2023
Số tiền bán 30 túi xách (lãi 20%):
100000 . 30 + 100000.30.20% = 3600000 (đồng)
Số tiền bán 20 túi xách (lỗ 10%):
20 . 100000 - 20.100000.10% = 1800000 (đồng)
Tổng số tiền bán được:
3600000 + 1800000 = 5400000 (đồng)
Tổng số tiền mua:
100000 . 50 = 5000000 (đồng)
Do 5400000 > 5000000 nên cửa hàng lời số tiền là:
5400000 - 5000000 = 400000 (đồng)
ko giúp thì thôi có cần đối xử như vậy ko Nguyễn Hải Dương
10 tháng 8 2016
Để \(\frac{4n+3}{3n+1}\) thuộc Z thì 4n + 3 chia hết cho 3n + 1
\(\Rightarrow3\left(4n+3\right)⋮3n+1\)
\(\Rightarrow12n+9⋮3n+1\)
\(\Rightarrow\left(12n+4\right)+5⋮3n+1\)
\(\Rightarrow4\left(3n+1\right)+5⋮3n+1\)
\(\Rightarrow5⋮3n+1\)
\(\Rightarrow3n+1\in\left\{\pm1;\pm5\right\}\)
+) 3n + 1 = 1\(\Rightarrow n=0\) ( chọn )
+) \(3n+1=-1\Rightarrow n=\frac{-2}{3}\) ( loại )
+) \(3n+1=5\Rightarrow n=\frac{4}{3}\) ( loại )
+) \(3n+1=-5\Rightarrow n=-2\)
Vậy n = 0 hoặc n = -2
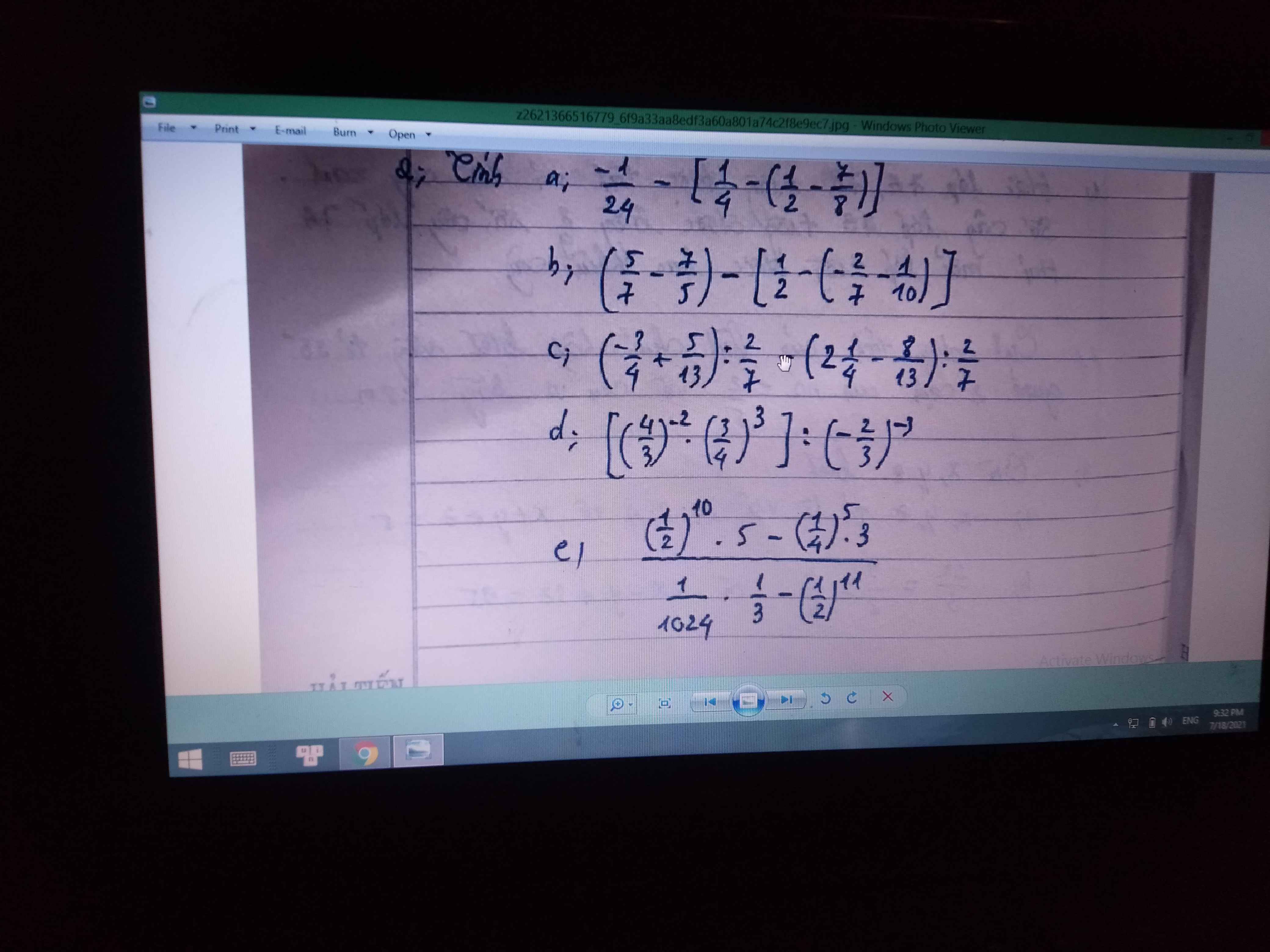
a) Ta có: \(\dfrac{-1}{24}-\left[\dfrac{1}{4}-\left(\dfrac{1}{2}-\dfrac{7}{8}\right)\right]\)
\(=\dfrac{-1}{24}-\left(\dfrac{1}{4}-\dfrac{1}{2}+\dfrac{7}{8}\right)\)
\(=\dfrac{-1}{24}-\dfrac{1}{4}+\dfrac{1}{2}-\dfrac{7}{8}\)
\(=\dfrac{-1}{24}-\dfrac{6}{24}+\dfrac{12}{24}-\dfrac{21}{24}\)
\(=\dfrac{-16}{24}=\dfrac{-2}{3}\)
b) Ta có: \(\left(\dfrac{5}{7}-\dfrac{7}{5}\right)-\left[\dfrac{1}{2}-\left(\dfrac{-2}{7}-\dfrac{1}{10}\right)\right]\)
\(=\dfrac{25-49}{35}-\left(\dfrac{1}{2}+\dfrac{2}{7}+\dfrac{1}{10}\right)\)
\(=\dfrac{-24}{35}-\dfrac{1}{2}-\dfrac{2}{7}-\dfrac{1}{10}\)
\(=\dfrac{-48}{70}-\dfrac{35}{70}-\dfrac{20}{70}-\dfrac{7}{70}\)
\(=\dfrac{-110}{70}=\dfrac{-11}{7}\)