
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


xy + 2x + y = 11
<=> x(y + 2) + y + 2 = 13
<=> (x + 1)(y + 2) = 13
Lập bảng xét các trường hợp
| x + 1 | 1 | 13 | -1 | -13 |
| y + 2 | 13 | 1 | -13 | -1 |
| x | 0 | 12 | -2 | -14 |
| y | 11 | -1 | -15 | -3 |
Vậy các cặp (x;y) thỏa là (0;11) ; (12 - 1) ; (-2;-15) ; (-14 ; -3)

ôi bn ơi k đc cho 5 ng mà bn lm thế nào k cho cả sever vn

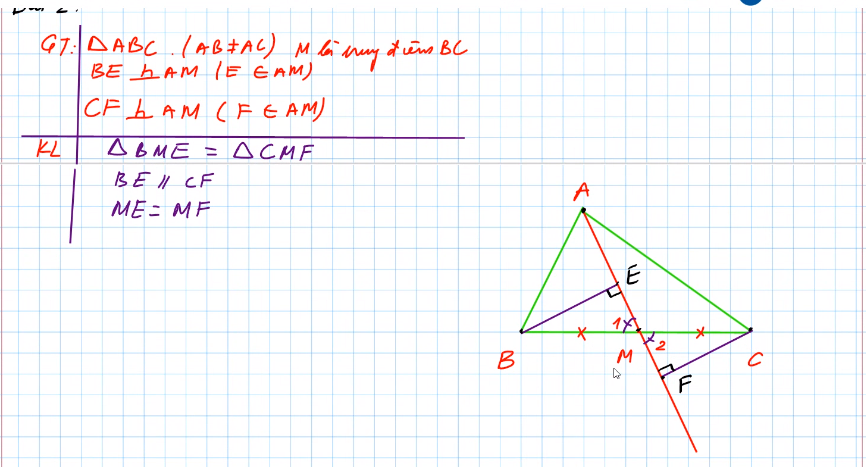
a: Xét ΔBME vuông tại E và ΔCMF vuông tại F có
MB=MC
\(\widehat{BME}=\widehat{CMF}\)
Do đó: ΔBME=ΔCMF
Suy ra: ME=MF
b: Xét tứ giác BECF có
M là trung điểm của BC
M là trung điểm của FE
Do đó: BECF là hình bình hành
Suy ra: BE//CF

a: NK=15cm
b: Xét ΔMNK vuông tại M và ΔMIK vuông tại M có
MK chung
MN=MI
Do đó: ΔMNK=ΔMIK
Suy ra: KN=KI
hay ΔKNI cân tại K
c: Xét ΔMAK vuông tại A và ΔMBK vuông tại B có
KM chung
\(\widehat{AKM}=\widehat{BKM}\)
Do đó: ΔMAK=ΔMBK
Suy ra: KA=KB
Xét ΔKIN có
KB/KI=KA/KN
Do đó: AB//IN

a: Xét ΔABD và ΔCBD có
BA=BC
\(\widehat{ABD}=\widehat{CBD}\)
BD chung
Do đó: ΔABD=ΔCBD
Suy ra: AD=CD


Bạn ơi , bạn xem lại đề nhé! Mình làm thế này không biết có đúng đề không nữa?
Ta có \(a^2+c^2\ge0\) (gt) mà \(a^2\ge0 \forall a, c^2\ge0 \forall c\)=> \(a\ne0 , c\ne0\)=> \(b\ne0\)( vì \(ab=c^2\))
Với \(a,b,c \ne0\), \(ab=c^2\)=> \(\frac{a}{c}=\frac{c}{b}\)
=> \(\left(\frac{a}{c}\right)^2=\left(\frac{c}{b}\right)^2\)
=> \(\frac{a^2}{c^2}=\frac{c^2}{b^2}=\frac{a^2+c^2}{c^2+b^2}\) mà \(\frac{a}{c}=\frac{c}{b}\)
=> \(\frac{a^2+c^2}{c^2+b^2}=\frac{a}{c}.\frac{c}{b}=\frac{a}{b}\)


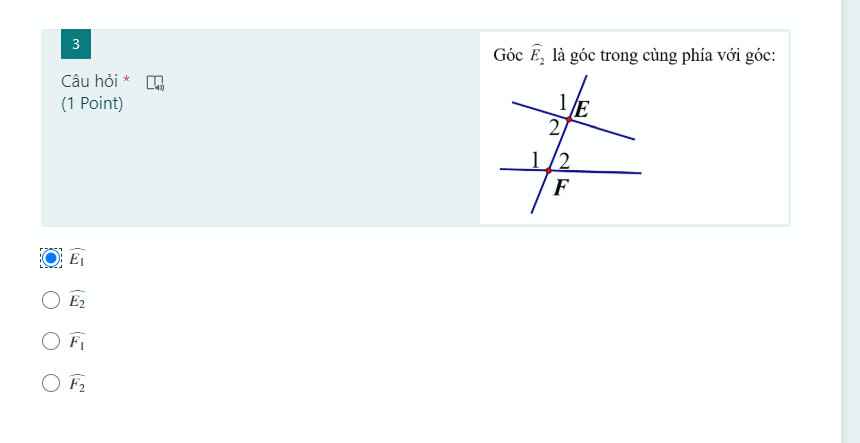 help tui có làm đk
help tui có làm đk HELP ME TUI ĐANG CẦN GẤP !!!
HELP ME TUI ĐANG CẦN GẤP !!!