
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét ΔADM và ΔCBN có
AD=CB
\(\widehat{DAM}=\widehat{BCN}\)
AM=CN
Do đó: ΔADM=ΔCBN
Suy ra: DM=BN


Em cần giúp câu nào hả em? Em nên chụp 1-2 ý cho 1 lần hỏi nhá, như thế mọi người sẽ dễ dàng giúp em hơn
13
a, \(3x-4=-x+8\)
\(< =>3x+x=8+4\)
\(< =>4x=12\)
\(< =>x=\frac{12}{4}=3\)
b, \(\frac{2x+1}{6}+\frac{x-7}{12}=10\)
\(< =>\frac{2\left(2x+1\right)}{12}+\frac{x-7}{12}=\frac{120}{12}\)
\(< =>4x+2+x-7=120\)
\(< =>5x=120+5=125\)
\(< =>x=\frac{125}{5}=\frac{5^3}{5}=5^2=25\)

a: \(A=\dfrac{6}{x-3}+\dfrac{2x^2}{x^2-1}+\dfrac{6-2x}{\left(x-3\right)\left(x^2-1\right)}\)
\(=\dfrac{6x^2-6+2x^3-6x^2+6-2x}{\left(x-3\right)\left(x^2-1\right)}\)
\(=\dfrac{2x^3-2x}{\left(x-3\right)\left(x^2-1\right)}=\dfrac{2x}{x-3}\)
b: Để A nguyên thì \(x-3\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
hay \(x\in\left\{4;2;5;6;0;9;-3\right\}\)
c: Thay x=2 vào A, ta được:
\(A=\dfrac{2\cdot2}{2-3}=-4\)
Thay x=-2 vào A, ta được:
\(A=\dfrac{-2\cdot2}{-2-3}=\dfrac{-4}{-5}=\dfrac{4}{5}\)

Bài 1:
Đáp số: 12 kệ thuốc, 10 thùng thuốc
Vì khi cho 2 thùng lên 1 kệ thì thừa 7 kệ(gt)
=> Số kệ >7
Theo công thức: số kệ = thùng : 2+ 7
Vì khi 1 thùng để lên 2 kệ thì thừa 4 thùng (gt)
=> Số thùng >4
Theo công thức: số thùng= thùng : 2 + 4
Từ đó, ta có thể suy ra được đáp số bằng cách rút gọn các số và cách giải cụ thể (hãy hỏi cô giáo)

\(4x^2-9=\left(2x\right)^2-3^2=\left(2x-3\right)\left(2x+3\right)\)
\(16x^2-8x+1=\left(4x\right)^2-2.4x.1+1=\left(4x-1\right)^2\)
\(x^3-1=\left(x-1\right)\left(x^2+x+1\right)\)
\(xy-xz+y-z=x\left(y-z\right)+\left(y-z\right)=\left(y-z\right)\left(x+1\right)\)

\(\dfrac{7x-2}{3}-2x< 5-\dfrac{x-2}{4}\)
<=>\(\dfrac{4\left(7x-2\right)}{12}-\dfrac{24x}{12}< \dfrac{60}{12}-\dfrac{3\left(x-2\right)}{12}\)
<=>\(4\left(7x-2\right)-24x< 60-3\left(x-2\right)\)
<=>\(28x-8-24x< 60-3x+6\)
<=>\(28x+3x-24x< 60+8+6\)
<=>\(7x< 74\)
<=>x<\(\dfrac{74}{7}\)
Vậy...

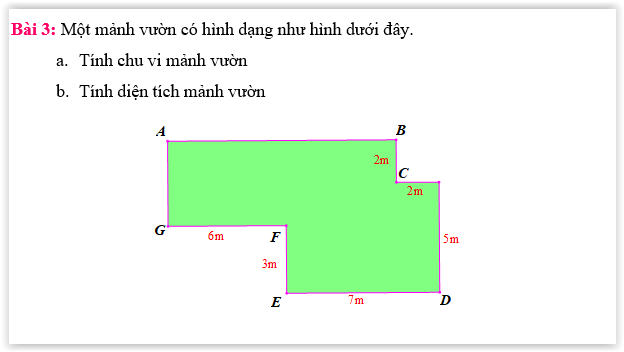


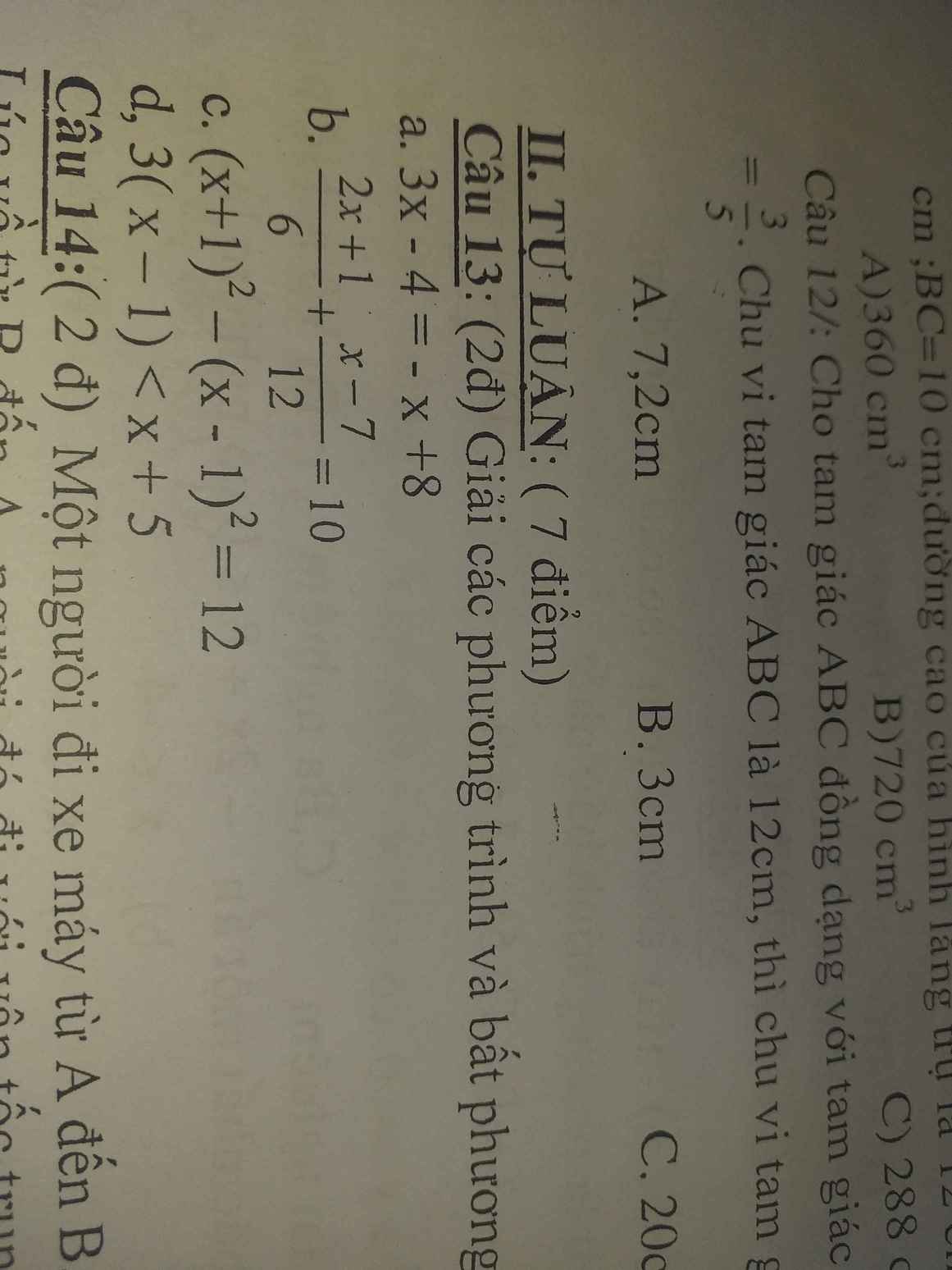


 giúp mk với ạ, mk đng cần gấp
giúp mk với ạ, mk đng cần gấp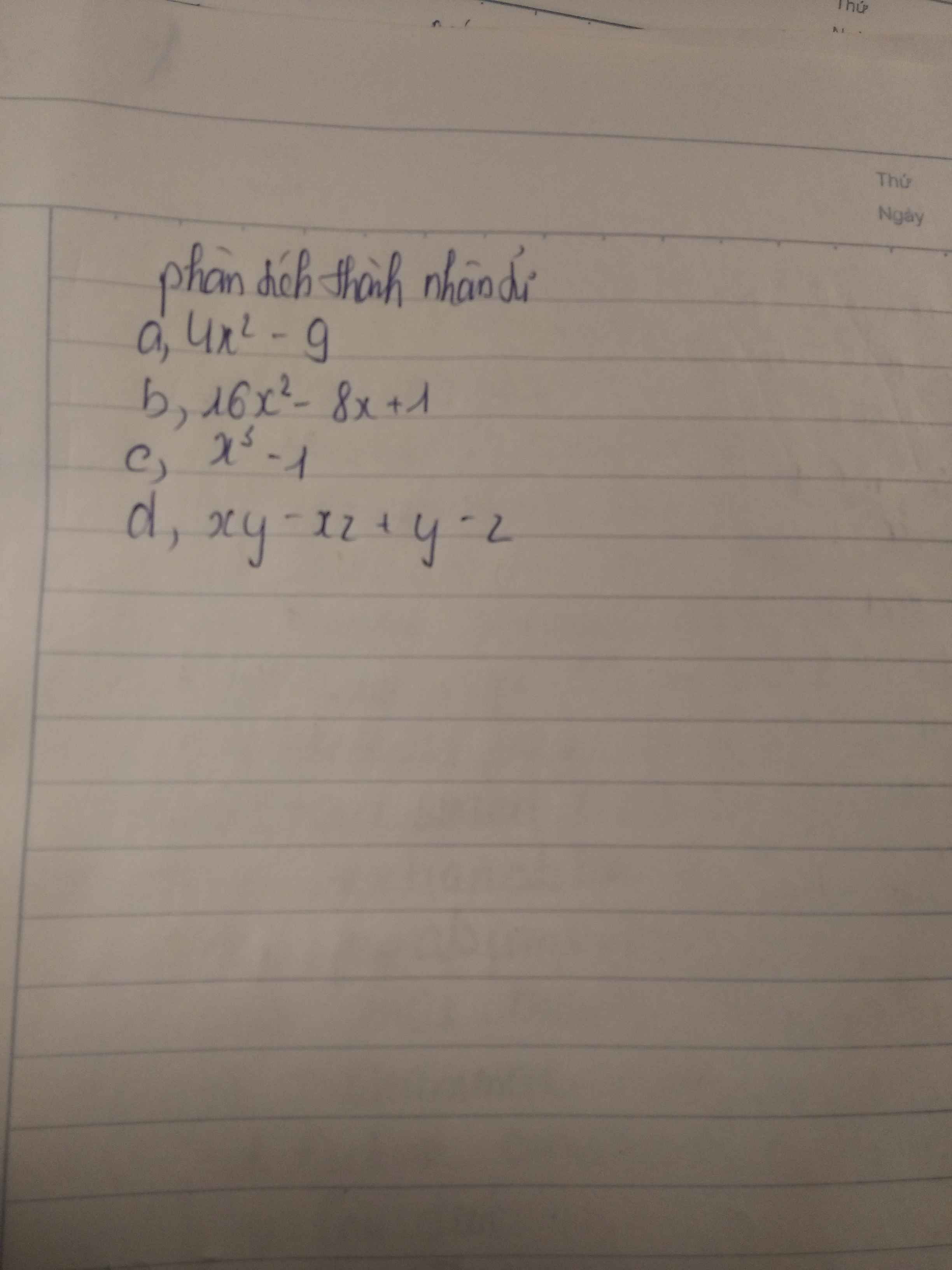


ta có
\(\text{2ap + bc = 2p.a + bc = (a + b + c).a + bc }\\ =a^2+ab+ca+bc\\ =a\left(a+b\right)+c\left(a+b\right)=\left(a+b\right)\left(a+c\right)\)
tương tự ta có
\(\left\{{}\begin{matrix}2pb+ac=\left(b+a\right)\left(b+c\right)\\2pc+ab=\left(c+a\right)\left(c+b\right)\end{matrix}\right.\)
\(\Rightarrow\left(2pa+bc\right)\left(2pb+ac\right)\left(2pc+ab\right)=\left(a+b\right)\left(c+a\right)\left(a+b\right)\left(b+c\right)\left(c+a\right)\left(b+c\right)=\left(a+b\right)^2\left(b+c\right)^2\left(c+a\right)^2\)