
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với `x >= 0,x ne 1` có:
Bth`=[2x+4+(\sqrt{x}+2)(\sqrt{x}-1)-2(x+\sqrt{x}+1)]/[(\sqrt{x}-1)(x+\sqrt{x}+1)]`
`=[2x+4+x-\sqrt{x}+2\sqrt{x}-2-2x-2\sqrt{x}-2]/[(\sqrt{x}-1)(x+\sqrt{x}+1)]`
`=[x-\sqrt{x}]/[(\sqrt{x}-1)(x+\sqrt{x}+1)]`
`=[\sqrt{x}(\sqrt{x}-1)]/[(\sqrt{x}-1)(x+\sqrt{x}+1)]`
`=\sqrt{x}/[x+\sqrt{x}+1]`
= \(\dfrac{2x+4}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\) + \(\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\) - \(\dfrac{2x+2\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
= \(\dfrac{2x+4+x-\sqrt{x}+2\sqrt{x}-2-2x-2\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
= \(\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
= \(\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)

a/ \(=\sqrt{81-2.9.\sqrt{3}+3}=\sqrt{\left(9-\sqrt{3}\right)^2}=9-\sqrt{3}\)
b/ \(=\frac{1}{\sqrt{2}}.\sqrt{14-6\sqrt{5}}=\frac{1}{\sqrt{2}}.\sqrt{9-2.3.\sqrt{5}+5}=\frac{1}{\sqrt{2}}\sqrt{\left(3-\sqrt{5}\right)^2}\)
\(=\frac{3-\sqrt{5}}{\sqrt{2}}=\frac{3\sqrt{2}-\sqrt{10}}{2}\)
c/ Ko khai phương được

câu a) bạn dựa vào đường cao nhé!(do góc bdc vuông, bec vuông)
b)bạn chỉ cần chứng minh adie là tứ giác nội tiếp ( adi+aei=180)
là có thề suy ra hai góc trên bằng nhau
Vì góc BOC= 180 độ=> sđ cung BC=180 độ => góc BEC=180/2=90 độ => BE vuông góc với AC=> BE là đường cao. Tương tự: có góc BDC=90 độ => DC là đường cao của tam giác ABC. Mà I là giao điểm của BE và CD => AI vuông góc với BC

Gọi x(sản phẩm) là số sản phẩm tổ sản xuất hoàn thành theo kế hoạch mỗi ngày. ĐK: x>0.
Ta có pt: \(\frac{800}{x}-2=\frac{800}{x+20}\)
\(\Leftrightarrow\frac{800-2x}{x}=\frac{800}{x+20}\)
\(\Rightarrow\left(800-2x\right)\left(x+20\right)=800x\)
\(\Leftrightarrow-2x^2-40x+16000=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=80\left(TM\right)\\x=-100\left(KTM\right)\end{matrix}\right.\)
Vậy năng suất mỗi ngày theo kế hoạch là 80 sản phẩm.
Gọi số sp theo kế hoạch tổ đó làm là : x (sản phẩm) (x > 0, x \(\in\) Z )
Theo kế hoạch, mỗi ngày tổ đó làm: \(\frac{800}{x}\) (sản phẩm)
Theo đề, ta có hệ phương trình:
\(\frac{800}{x+20}+2=\frac{800}{x}\) ==> x= 80 => mỗi ngày theo kế hoạch cần làm 10 sản phẳm

\(< =>\hept{\begin{cases}2xy+y+2x+1=2x^2\\2xy+x+2y+1=8xy+10x-12y-15\end{cases}+3x}\)

Gọi số ngày đội 1,2 làm là x,y. ĐK: \(0< x< y\)
Mỗi ngày hai đội làm được : \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\)(công việc)(1)
Vì thời gian đội 1 làm ít hơn đội 2 là 6h=\(\dfrac{1}{4}\)ngày nên ta có: \(x+\dfrac{1}{4}=y\)
Thay vào (1), ta có: \(\dfrac{1}{x}+\dfrac{1}{x+\dfrac{1}{4}}=\dfrac{1}{4}\)
\(\Rightarrow4x^2-31x-4=0\)
\(\Rightarrow x=\dfrac{31+5\sqrt{41}}{8}\) thỏa mãn.
\(\Rightarrow y=\dfrac{33+5\sqrt{41}}{8}\)(TM).
Vậy đội 1 làm xong công việc 1 mình mất \(\dfrac{31+5\sqrt{41}}{8}\) ngày, đội 2 làm mất \(\dfrac{33+5\sqrt{41}}{8}\) ngày.

\(A=\dfrac{x+1}{2x-2}+\dfrac{x^2+3}{2-2x^2}+\dfrac{1}{1-x}-15\)
\(A=\dfrac{x+1}{2.\left(x-1\right)}+\dfrac{x^2+3}{2.\left(1-x\right).\left(1+x\right)}+\dfrac{1}{1-x}-\dfrac{15}{1}\)
\(A=\dfrac{\left(x+1\right)^2-\left(x^2+3\right)-2.\left(x+1\right)-15.2.\left(x-1\right).\left(x+1\right)}{2.\left(x-1\right).\left(x+1\right)}\)
\(A=\dfrac{x^2+2x+1-x^2-3-2x-30.\left(x^2-1\right)}{2.\left(x-1\right).\left(x+1\right)}\)
\(A=\dfrac{-4-30x^2+30}{2.\left(x-1\right).\left(x+1\right)}\)
\(A=\dfrac{26-30x^2}{2.\left(x-1\right).\left(x+1\right)}\)
\(A=\dfrac{2.\left(13-15x^2\right)}{2.\left(x-1\right).\left(x+1\right)}\)
\(A=\dfrac{13-15x^2}{\left(x-1\right).\left(x+1\right)}\)
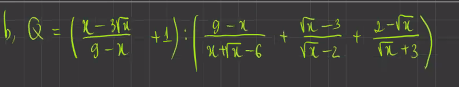
ĐK: \(x\ge0;x\ne4;x\ne9\)
\(Q=\left(\dfrac{x-3\sqrt{x}}{9-x}+1\right):\left(\dfrac{9-x}{x+\sqrt{x}-6}+\dfrac{\sqrt{x}-3}{\sqrt{x}-2}+\dfrac{2-\sqrt{x}}{\sqrt{x}+3}\right)\)
\(=\left[-\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+1\right]:\left[\dfrac{9-x}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}+\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}+\dfrac{\left(2-\sqrt{x}\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\right]\)
\(=\dfrac{3}{\sqrt{x}+3}:\dfrac{-\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3}{\sqrt{x}+3}.\dfrac{-\left(\sqrt{x}+3\right)}{\sqrt{x}-2}\)
\(=\dfrac{3}{2-\sqrt{x}}\)